Iteration History :: SAS/ETS(R) 13.1 User's Guide

ITPRINT Option

The ITPRINT information is selected whenever any iteration information is requested.

The following information is displayed for each iteration:

N: is the number of usable observations.
Objective: is the corrected objective function value.
Trace(S): is the trace of the S matrix.
subit: is the number of subiterations required to find a 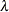${\lambda }$ or a damping factor that reduces the objective function.
R: is the R convergence measure.

The estimates for the parameters at each iteration are also printed.

ITDETAILS Option

The additional values printed for the ITDETAILS option are:

Theta: is the angle in degrees between 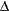${\Delta }$ , the parameter change vector, and the negative gradient of the objective function.
Phi: is the directional derivative of the objective function in the 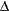${\Delta }$ direction scaled by the objective function.
Stepsize: is the value of the damping factor used to reduce 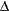${\Delta }$ if the Gauss-Newton method is used.
Lambda: is the value of 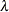${\lambda }$ if the Marquardt method is used.
Rank(XPX): is the rank of the 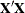${\mb {X} ’\mb {X} }$ matrix (output if the projected Jacobian crossproducts matrix is singular).

The definitions of PPC and R are explained in the section Convergence Criteria. When the values of PPC are large, the parameter associated with the criteria is displayed in parentheses after the value.

XPX and I Options

The XPX and the I options select the printing of the augmented ${\mb {X} ’\mb {X} }$ matrix and the augmented ${\mb {X} ’\mb {X} }$ matrix after a sweep operation (Goodnight, 1979) has been performed on it. An example of the output from the following statements is shown in Figure 19.36.

proc model data=test2;
   y1 = a1 * x2 * x2 - exp( d1*x1);
   y2 = a2 * x1 * x1 + b2 * exp( d2*x2);
   fit y1 y2 / itall XPX I ;
run;

Figure 19.36: XPX and I Options Output

The MODEL Procedure

OLS Estimation

Cross Products for System At OLS Iteration 0
	a1	d1	a2	b2	d2	Residual
a1	1839468	-33818.35	0.0	0.00	0.000000	3879959
d1	-33818	1276.45	0.0	0.00	0.000000	-76928
a2	0	0.00	42925.0	1275.15	0.154739	470686
b2	0	0.00	1275.2	50.01	0.003867	16055
d2	0	0.00	0.2	0.00	0.000064	2
Residual	3879959	-76928.14	470686.3	16055.07	2.329718	24576144

XPX Inverse for System At OLS Iteration 0
	a1	d1	a2	b2	d2	Residual
a1	0.000001	0.000028	0.000000	0.0000	0.00	2
d1	0.000028	0.001527	0.000000	0.0000	0.00	-9
a2	0.000000	0.000000	0.000097	-0.0025	-0.08	6
b2	0.000000	0.000000	-0.002455	0.0825	0.95	172
d2	0.000000	0.000000	-0.084915	0.9476	15746.71	11931
Residual	1.952150	-8.546875	5.823969	171.6234	11930.89	10819902

The first matrix, labeled “Cross Products,” for OLS estimation is

$\begin{eqnarray*} \left[ \begin{matrix} \Strong{X} ’\Strong{X} & \Strong{X} ’\Strong{r} \\ \Strong{r} ’\Strong{X} & \Strong{r} ’\Strong{r} \end{matrix} \right] \nonumber \end{eqnarray*}$

The column labeled Residual in the output is the vector ${\mb {X} ’\mb {r} }$ , which is the gradient of the objective function. The diagonal scalar value $\mb {r} {’}\mb {r}$ is the objective function uncorrected for degrees of freedom. The second matrix, labeled “XPX Inverse,” is created through a sweep operation on the augmented ${\mb {X} ’\mb {X} }$ matrix to get:

$\begin{eqnarray*} \left[ \begin{matrix} (\Strong{X} ’\Strong{X} )^{-1} & (\Strong{X} ’\Strong{X} )^{-1}\Strong{X} ’\Strong{r} \\ (\Strong{X} ’\Strong{r} )’(\Strong{X} ’\Strong{X} )^{-1} & \Strong{r} ’\Strong{r} -(\Strong{X} ’\Strong{r} )’(\Strong{X} ’\Strong{X} )^{-1}\Strong{X} ’\Strong{r} \end{matrix} \right] \nonumber \end{eqnarray*}$

Note that the residual column is the change vector used to update the parameter estimates at each iteration. The corner scalar element is used to compute the R convergence criteria.

ITALL Option

The ITALL option, in addition to causing the output of all of the preceding options, outputs the S matrix, the inverse of the S matrix, the CROSS matrix, and the swept CROSS matrix. An example of a portion of the CROSS matrix for the preceding example is shown in Figure 19.37.

Figure 19.37: ITALL Option Crossproducts Matrix Output

The MODEL Procedure

OLS Estimation

Crossproducts Matrix At OLS Iteration 0
	1	@PRED.y1/@a1	@PRED.y1/@d1	@PRED.y2/@a2	@PRED.y2/@b2	@PRED.y2/@d2	RESID.y1	RESID.y2
1	50.00	6409	-239.16	1275.0	50.00	0.003803	14700	16053
@PRED.y1/@a1	6409.08	1839468	-33818.35	187766.1	6409.88	0.813934	3879959	4065028
@PRED.y1/@d1	-239.16	-33818	1276.45	-7253.0	-239.19	-0.026177	-76928	-85084
@PRED.y2/@a2	1275.00	187766	-7253.00	42925.0	1275.15	0.154739	420583	470686
@PRED.y2/@b2	50.00	6410	-239.19	1275.2	50.01	0.003867	14702	16055
@PRED.y2/@d2	0.00	1	-0.03	0.2	0.00	0.000064	2	2
RESID.y1	14699.97	3879959	-76928.14	420582.9	14701.77	1.820356	11827102	12234106
RESID.y2	16052.76	4065028	-85083.68	470686.3	16055.07	2.329718	12234106	12749042