Example 19.13 Switching Regression Example :: SAS/ETS(R) 13.1 User's Guide

Example 19.13 Switching Regression Example

Take the usual linear regression problem

$y \; = \; \bX \beta \; + \; u$

where Y denotes the n column vector of the dependent variable, ${\bX }$ denotes the (n $\times$ k ) matrix of independent variables, $\beta$ denotes the k column vector of coefficients to be estimated, n denotes the number of observations (i =1, 2, …, n ), and k denotes the number of independent variables.

You can take this basic equation and split it into two regimes, where the ith observation on y is generated by one regime or the other:

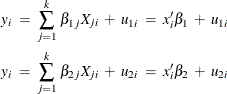
$\begin{eqnarray*} y_{i} \; = \; \sum _{j=1}^{k} \, \beta _{1j} X_{ji} \; + \; u_{1i} \; = \; x_{i}’ \beta _{1} \; + \; u_{1i} \\ y_{i} \; = \; \sum _{j=1}^{k} \, \beta _{2j} X_{ji} \; + \; u_{2i} \; = \; x_{i}’ \beta _{2} \; + \; u_{2i} \end{eqnarray*}$

where $x_{hi}$ and $x_{hj}$ are the ith and jth observations, respectively, on $x_{h}$ . The errors, $u_{1i}$ and $u_{2i}$ , are assumed to be distributed normally and independently with mean zero and constant variance. The variance for the first regime is $\sigma _{1}^{2}$ , and the variance for the second regime is $\sigma _{2}^{2}$ . If $\sigma _{1}^{2} \neq \sigma _{2}^{2}$ and $\beta _{1} \neq \beta _{2}$ , the regression system given previously is thought to be switching between the two regimes.

The problem is to estimate $\beta _{1}$ , $\beta _{2}$ , $\sigma _{1}$ , and $\sigma _{2}$ without knowing a priori which of the n values of the dependent variable, y, was generated by which regime. If it is known a priori which observations belong to which regime, a simple Chow test can be used to test $\sigma _{1}^{2} = \sigma _{2}^{2}$ and $\beta _{1} = \beta _{2}$ .

Using Goldfeld and Quandt’s D-method for switching regression, you can solve this problem. Assume that observations exist on some exogenous variables $z_{1i}, \, z_{2i}, \, \ldots , \, z_{pi}$ , where z determines whether the ith observation is generated from one equation or the other. The equations are given as follows:

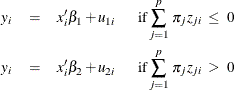
$\begin{eqnarray*} y_{i} & = & x_{i}’ \beta _{1} + u_{1i} ~ ~ ~ ~ ~ ~ \mbox{if} \sum _{j=1}^{p} \, \pi _{j} z_{ji} \; \leq \; 0 \\ y_{i} & = & x_{i}’ \beta _{2} + u_{2i} ~ ~ ~ ~ ~ ~ \mbox{if} \sum _{j=1}^{p} \, \pi _{j} z_{ji} \; > \; 0 \end{eqnarray*}$

where $\pi _{j}$ are unknown coefficients to be estimated. Define $d(z_{i})$ as a continuous approximation to a step function. Replacing the unit step function with a continuous approximation by using the cumulative normal integral enables a more practical method that produces consistent estimates.

$d(z_{i}) \; = \; \frac{1}{\sqrt {2 \pi } \sigma } \, \int _{- \infty }^{\sum \pi _{j} z_{ji}} \, exp \left[ - \frac{1}{2} \, \frac{\xi ^{2}}{\sigma ^{2}} \right] \, d \xi$

${\bD }$ is the n dimensional diagonal matrix consisting of $d(z_{i})$ :

$\bD \; = \; \left[ \begin{array}{cccc} d(z_{1}) & 0 & 0 & 0 \\ 0 & d(z_{2}) & 0 & 0 \\ 0 & 0 & \ddots & 0 \\ 0 & 0 & 0 & d(z_{n}) \end{array} \right]$

The parameters to estimate are now the k $\beta _{1}$ ’s, the k $\beta _{2}$ ’s, $\sigma _{1}^{2}$ , $\sigma _{2}^{2}$ , p $\pi$ ’s, and the $\sigma$ introduced in the $d(z_ i)$ equation. The $\sigma$ can be considered as given a priori, or it can be estimated, in which case, the estimated magnitude provides an estimate of the success in discriminating between the two regimes (Goldfeld and Quandt, 1976). Given the preceding equations, the model can be written as:

$Y = ({\bI } \, - \, \bD ) \, {\bX } \beta _{1} + {\bD } {\bX } \beta _{2} + W$

where $W \, = \, ({\bI } - {\bD }) U_{1} \, + \, {\bD } U_{2}$ , and W is a vector of unobservable and heteroscedastic error terms. The covariance matrix of W is denoted by $\bOmega$ , where $\bOmega \, = \, ({\bI }-{\bD })^2 \sigma _{1}^{2} \, + \, {\bD }^2 \sigma _{2}^{2 }$ . The maximum likelihood parameter estimates maximize the following log-likelihood function.

$\begin{eqnarray*} \log L & = & - \frac{n}{2} \log 2 \pi - \frac{1}{2} \log \mid \bOmega \mid - \nonumber \\ & & \frac{1}{2} * \left[ \left[ Y - ({\bI } - {\bD }) {\bX } \beta _{1} - {\bD } {\bX } \beta _{2} \right] ’ \bOmega ^{-1} \left[ Y - ({\bI } - {\bD }) {\bX } \beta _{1} - {\bD } {\bX } \beta _{2} \right] \right] \nonumber \end{eqnarray*}$

As an example, you now can use this switching regression likelihood to develop a model of housing starts as a function of changes in mortgage interest rates. The data for this example are from the U.S. Census Bureau and cover the period from January 1973 to March 1999. The hypothesis is that there are different coefficients on your model based on whether the interest rates are going up or down.

So the model for $z_ i$ is

$z_ i = p * ( \mr {rate}_ i - \mr {rate}_{i-1} )$

where $\mr {rate}_ i$ is the mortgage interest rate at time $i$ and $p$ is a scale parameter to be estimated.

The regression model is

$\begin{eqnarray*} \mr {starts}_ i & =& \mr {intercept}_1 + \mr {ar}1 * \mr {starts}_{i-1} + \mr {djf}1 * \mr {decjanfeb} ~ ~ ~ ~ ~ ~ ~ ~ ~ z_ i < 0 \\ \mr {starts}_ i & =& \mr {intercept}_2 + \mr {ar}2 * \mr {starts}_{i-1} + \mr {djf}2 * \mr {decjanfeb} ~ ~ ~ ~ ~ ~ ~ ~ ~ z_ i > = 0 \end{eqnarray*}$

where $\mr {starts}_ i$ is the number of housing starts at month $i$ and $\mr {decjanfeb}$ is a dummy variable that indicates that the current month is one of December, January, or February.

This model is written by using the following SAS statements:

title1 'Switching Regression Example';

proc model data=switch;
   parms sig1=10 sig2=10 int1 b11 b13 int2 b21 b23 p;
   bounds 0.0001 < sig1 sig2;

   decjanfeb = ( month(date) = 12 | month(date) <= 2 );

   a = p*dif(rate);       /* Upper bound of integral */
   d = probnorm(a);       /* Normal CDF as an approx of switch */

                          /* Regime 1 */
   y1 = int1 + zlag(starts)*b11 + decjanfeb *b13 ;
                          /* Regime 2 */
   y2 = int2 + zlag(starts)*b21 + decjanfeb *b23 ;
                          /* Composite regression equation */
   starts  = (1 - d)*y1 +  d*y2;

                         /* Resulting log-likelihood function */
   logL = (1/2)*( (log(2*3.1415)) +
        log( (sig1**2)*((1-d)**2)+(sig2**2)*(d**2) )
       + (resid.starts*( 1/( (sig1**2)*((1-d)**2)+
        (sig2**2)*(d**2) ) )*resid.starts) ) ;

   errormodel starts ~ general(logL);

   fit starts / method=marquardt converge=1.0e-5;

     /* Test for significant differences in the parms */
   test int1 = int2 ,/ lm;
   test b11 = b21 ,/ lm;
   test b13 = b23 ,/ lm;
   test sig1 = sig2 ,/ lm;

run;

Four TEST statements are added to test the hypothesis that the parameters are the same in both regimes. The parameter estimates and ANOVA table from this run are shown in Output 19.13.1.

Output 19.13.1: Parameter Estimates from the Switching Regression

Switching Regression Example

The MODEL Procedure

Nonlinear Liklhood Summary of Residual Errors
Equation	DF Model	DF Error	SSE	MSE	Root MSE	R-Square	Adj R-Sq	Label
starts	9	304	85878.0	282.5	16.8075	0.7806	0.7748	Housing Starts

Nonlinear Liklhood Parameter Estimates
Parameter	Estimate	Approx Std Err	t Value	Approx Pr > \|t\|
sig1	15.47484	0.9476	16.33	<.0001
sig2	19.77808	1.2710	15.56	<.0001
int1	32.82221	5.9083	5.56	<.0001
b11	0.73952	0.0444	16.64	<.0001
b13	-15.4556	3.1912	-4.84	<.0001
int2	42.73348	6.8159	6.27	<.0001
b21	0.734117	0.0478	15.37	<.0001
b23	-22.5184	4.2985	-5.24	<.0001
p	25.94712	8.5205	3.05	0.0025

The test results shown in Output 19.13.2 suggest that the variance of the housing starts, SIG1 and SIG2, are significantly different in the two regimes. The tests also show a significant difference in the AR term on the housing starts.

Output 19.13.2: Test Results for Switching Regression

Test Results
Test	Type	Statistic	Pr > ChiSq	Label
Test0	L.M.	1.00	0.3185	int1 = int2
Test1	L.M.	15636	<.0001	b11 = b21
Test2	L.M.	1.45	0.2280	b13 = b23
Test3	L.M.	4.39	0.0361	sig1 = sig2