The MODEL Procedure

Solution Modes

Subsections:

Dynamic and Static Simulations
n-Period-Ahead Forecasting
Simulation and Forecasting
Monte Carlo Simulation

The following solution modes are commonly used:

The dynamic simultaneous forecast mode is used for forecasting with the model. Collect the historical data on the model variables, the future assumptions of the exogenous variables, and any prior information on the future endogenous values, and combine them in a SAS data set. Use the FORECAST option in the SOLVE statement.
The dynamic simultaneous simulation mode is often called ex post simulation, historical simulation, or ex post forecasting. Use the DYNAMIC option. This mode is the default.
The static simultaneous simulation mode can be used to examine the within-period performance of the model without the complications of previous period errors. Use the STATIC option.
The NAHEAD=n dynamic simultaneous simulation mode can be used to see how well n-period-ahead forecasting would have performed over the historical period. Use the NAHEAD=n option.

The different solution modes are explained in detail in the following sections.

Dynamic and Static Simulations

In model simulation, either solved values or actual values from the data set can be used to supply lagged values of an endogenous variable. A dynamic solution refers to a solution obtained by using only solved values for the lagged values. Dynamic mode is used both for forecasting and for simulating the dynamic properties of the model.

A static solution refers to a solution obtained by using the actual values when available for the lagged endogenous values. Static mode is used to simulate the behavior of the model without the complication of previous period errors. Dynamic simulation is the default.

If you want to use static values for lags only for the first n observations, and dynamic values thereafter, specify the START=n option. For example, if you want a dynamic simulation to start after observation twenty-four, specify START=24 on the SOLVE statement. If the model being simulated had a value lagged for four time periods, then this value would start using dynamic values when the simulation reached observation number 28.

n-Period-Ahead Forecasting

Suppose you want to regularly forecast 12 months ahead and produce a new forecast each month as more data becomes available. n-period-ahead forecasting allows you to test how well you would have done over time if you had been using your model to forecast one year ahead.

To see how well a model predicts n time periods in the future, perform an n-period-ahead forecast on real data and compare the forecast values with the actual values.

n-period-ahead forecasting refers to using dynamic values for the lagged endogenous variables only for lags 1 through n–1. For example, one-period-ahead forecasting, specified by the NAHEAD=1 option in the SOLVE statement, is the same as if a static solution had been requested. Specifying NAHEAD=2 produces a solution that uses dynamic values for lag one and static, actual, values for longer lags.

The following example is a two-year-ahead dynamic simulation. The output is shown in Figure 19.70.

data yearly;
   input year x1 x2 x3 y1 y2 y3;
   datalines;
84 4 9  0  7  4  5
85 5 6  1  1  27  4
86 3 8  2  5  8  2
87 2 10 3  0  10 10
88 4 7  6  20 60 40
89 5 4  8  40 40 40
90 3 2  10 50 60 60
91 2 5  11 40 50 60
;
run;

proc model data=yearly outmodel=yearlyModel;
   endogenous y1 y2 y3;
   exogenous  x1 x2 x3;

   y1 = 2 + 3*x1 - 2*x2 + 4*x3;
   y2 = 4 + lag2( y3 ) + 2*y1 + x1;
   y3 = lag3( y1 ) + y2 - x2;

   solve y1 y2 y3 / nahead=2 out=c;
run;

proc print data=c;
run;

Figure 19.70: NAHEAD Summary Report

The MODEL Procedure

Dynamic Simultaneous 2-Periods-Ahead Forecasting Simulation

Data Set Options
DATA=	YEARLY
OUT=	C

Solution Summary
Variables Solved	3
Simulation Lag Length	3
Solution Method	NEWTON
CONVERGE=	1E-8
Maximum CC	0
Maximum Iterations	1
Total Iterations	8
Average Iterations	1

Observations Processed
Read	20
Lagged	12
Solved	8
First	5
Last	8

Variables Solved For	y1 y2 y3

The C data set is shown in Figure 19.71:

Figure 19.71: C Data Set

Obs	_TYPE_	_MODE_	_LAG_	y1	y2	y3	x1	x2	x3
1	PREDICT	SIMULATE	0	0	10	7	2	10	3
2	PREDICT	SIMULATE	1	24	58	52	4	7	6
3	PREDICT	SIMULATE	1	41	101	102	5	4	8
4	PREDICT	SIMULATE	1	47	141	139	3	2	10
5	PREDICT	SIMULATE	1	42	130	145	2	5	11

The preceding two-year-ahead simulation can be emulated without using the NAHEAD= option by the following PROC MODEL statements:

proc model data=yearly model=yearlyModel;
  range year = 87 to 88;
  solve y1 y2 y3 / dynamic solveprint;
run;

  range year = 88 to 89;
  solve y1 y2 y3 / dynamic solveprint;
run;

  range year = 89 to 90;
  solve y1 y2 y3 / dynamic solveprint;
run;

  range year = 90 to 91;
  solve y1 y2 y3 / dynamic solveprint;

The totals shown under "Observations Processed" in Figure 19.70 are equal to the sum of the four individual runs.

Simulation and Forecasting

You can perform a simulation of your model or use the model to produce forecasts. Simulation refers to the determination of the endogenous or dependent variables as a function of the input values of the other variables, even when actual data for some of the solution variables are available in the input data set. The simulation mode is useful for verifying the fit of the model parameters. Simulation is selected by the SIMULATE option in the SOLVE statement. Simulation mode is the default.

In forecast mode, PROC MODEL solves only for those endogenous variables that are missing in the data set. The actual value of an endogenous variable is used as the solution value whenever nonmissing data for it is available in the input data set. Forecasting is selected by the FORECAST option in the SOLVE statement.

For example, an econometric forecasting model can contain an equation to predict future tax rates, but tax rates are usually set in advance by law. Thus, for the first year or so of the forecast, the predicted tax rate should really be exogenous. Or, you might want to use a prior forecast of a certain variable from a short-run forecasting model to provide the predicted values for the earlier periods of a longer-range forecast of a long-run model. A common situation in forecasting is when historical data needed to fill the initial lags of a dynamic model are available for some of the variables but have not yet been obtained for others. In this case, the forecast must start in the past to supply the missing initial lags. Clearly, you should use the actual data that are available for the lags. In all the preceding cases, the forecast should be produced by running the model in the FORECAST mode; simulating the model over the future periods would not be appropriate.

Monte Carlo Simulation

The accuracy of the forecasts produced by PROC MODEL depends on four sources of error (Pindyck and Rubinfeld, 1981, pp. 405–406):

The system of equations contains an implicit random error term ${\epsilon }$

$\mb{g} (\mb{y} ,\mb{x} ,\hat{{{\btheta }}})={{\bepsilon }}$

where y, x, g, 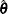$\hat{\btheta }$ , and $\bepsilon$ are vector valued.
The estimated values of the parameters, 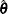$\hat{\btheta }$ , are themselves random variables.
The exogenous variables might have been forecast themselves and therefore might contain errors.
The system of equations might be incorrectly specified; the model only approximates the process modeled.

The RANDOM= option is used to request Monte Carlo (or stochastic) simulations to generate confidence intervals for errors that arise from the first two sources. The Monte Carlo simulations can be performed with $\bepsilon$ , $\btheta$ , or both vectors represented as random variables. The SEED= option is used to control the random number generator for the simulations. SEED=0 forces the random number generator to use the system clock as its seed value.

In Monte Carlo simulations, repeated simulations are performed on the model for random perturbations of the parameters and the additive error term. The random perturbations follow a multivariate normal distribution with expected value of 0 and covariance described by a covariance matrix of the parameter estimates in the case of ${\theta }$ , or a covariance matrix of the equation residuals for the case of ${\epsilon }$ . PROC MODEL can generate both covariance matrices or you can provide them.

The ESTDATA= option specifies a data set that contains an estimate of the covariance matrix of the parameter estimates to use for computing perturbations of the parameters. The ESTDATA= data set is usually created by the FIT statement with the OUTEST= and OUTCOV options. When the ESTDATA= option is specified, the matrix read from the ESTDATA= data set is used to compute vectors of random shocks or perturbations for the parameters. These random perturbations are computed at the start of each repetition of the solution and added to the parameter values. The perturbed parameters are fixed throughout the solution range. If the covariance matrix of the parameter estimates is not provided, the parameters are not perturbed.

The SDATA= option specifies a data set that contains the covariance matrix of the residuals to use for computing perturbations of the equations. The SDATA= data set is usually created by the FIT statement with the OUTS= option. When SDATA= is specified, the matrix read from the SDATA= data set is used to compute vectors of random shocks or perturbations for the equations. These random perturbations are computed at each observation. The simultaneous solution satisfies the model equations plus the random shocks. That is, the solution is not a perturbation of a simultaneous solution of the structural equations; rather, it is a simultaneous solution of the stochastic equations by using the simulated errors. If the SDATA= option is not specified, the random shocks are not used.

The different random solutions are identified by the _REP_ variable in the OUT= data set. An unperturbed solution with _REP_=0 is also computed when the RANDOM= option is used. RANDOM=n produces n +1 solution observations for each input observation in the solution range. If the RANDOM= option is not specified, the SDATA= and ESTDATA= options are ignored, and no Monte Carlo simulation is performed.

PROC MODEL does not have an automatic way of modeling the exogenous variables as random variables for Monte Carlo simulation. If the exogenous variables have been forecast, the error bounds for these variables should be included in the error bounds generated for the endogenous variables. If the models for the exogenous variables are included in PROC MODEL, then the error bounds created from a Monte Carlo simulation contain the uncertainty due to the exogenous variables.

Alternatively, if the distribution of the exogenous variables is known, the built-in random number generator functions can be used to perturb these variables appropriately for the Monte Carlo simulation. For example, if you know the forecast of an exogenous variable, X, has a standard error of 5.2 and the error is normally distributed, then the following statements can be used to generate random values for X:

   x_new = x + 5.2 * rannor(456);

During a Monte Carlo simulation, the random number generator functions produce one value at each observation. It is important to use a different seed value for all the random number generator functions in the model program; otherwise, the perturbations will be correlated. For the unperturbed solution, _REP_=0, the random number generator functions return 0.

PROC UNIVARIATE can be used to create confidence intervals for the simulation (see the Monte Carlo simulation example in the section Getting Started: MODEL Procedure).