What’s New in SAS/ETS 13.2
The following features have been added to the PANEL procedure:
-
First-differenced methods for one-way and two-way models. The first-differenced (FD) estimator is an approach that is often used to address the problem of omitted variables in econometrics and statistics by using the panel data approach. The estimator is obtained by running a pooled OLS estimation for a regression of the differenced variables. The FD estimator is obtained by specifying the FDONE, FDONETIME, or FDTWO option in the MODEL statement.
-
Panel data cross-sectional dependence test. You can request the panel data cross-sectional dependence tests by specifying the CDTEST option in the MODEL statement. These tests include the Breusch and Pagan (1980) LM test, the scaled version of the Breusch and Pagan (1980) test, and the Pesaran (2004) CD test. When you specify P=value, the CD test for local cross-sectional dependence is performed with the order
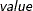 , where
, where 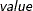 is an integer greater than zero.
is an integer greater than zero.
-
Lagrange multiplier (LM) tests for cross-sectional and time effects. The Breusch-Pagan LM test is two-sided when the variance components are nonnegative. For a one-sided alternative hypothesis, Honda (1985) suggests a uniformly most powerful (UMP) LM test for
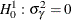 (no cross-sectional effects) that is based on the pooled estimator. The alternative is the one-sided
(no cross-sectional effects) that is based on the pooled estimator. The alternative is the one-sided 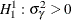 . Moulton and Randolph (1989) suggest an alternative standardized Lagrange multiplier (SLM) test to improve the asymptotic approximation for Honda’s one-sided
LM statistic. You can request the UMP and SLM tests for one-way and two-way random-effects models by specifying the HONDA
and HONDA2 options, respectively, in the MODEL statement.
. Moulton and Randolph (1989) suggest an alternative standardized Lagrange multiplier (SLM) test to improve the asymptotic approximation for Honda’s one-sided
LM statistic. You can request the UMP and SLM tests for one-way and two-way random-effects models by specifying the HONDA
and HONDA2 options, respectively, in the MODEL statement.
-
LMMP test and the SLM test. King and Wu (1997) derived the locally mean most powerful (LMMP) one-sided test, which coincides with the Honda (1985) UMP test and is extended by Baltagi, Chang, and Li (1992). You can request the King and Wu test by specifying the KW option.
-
Gourieroux, Holly, and Monfort (1982) LM test. In another extension Baltagi, Chang, and Li (1992) follow Gourieroux, Holly, and Monfort (1982) and propose a one-sided LM test that overcomes a possible problem with negative
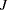 and
and 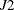 test statistics in the Honda test. You can request the test by specifying the GHM option.
test statistics in the Honda test. You can request the test by specifying the GHM option.
-
Tests for serial correlation and cross-sectional effects. The presence of cross-sectional effects causes serial correlation in the errors. Therefore, serial correlation is often tested jointly with cross-sectional effects. Baltagi and Li (1991) derive the LM test statistic, which jointly tests for zero first-order serial correlation and random cross-sectional effects under normality and homoscedasticity. You can obtain the Baltagi and Li (1991) test by specifying the BL91 option. Wooldridge (2002) suggests a test for the absence of unobserved effects, which can be obtained by specifying the WOOLDRIDGE02 option. Bera, Sosa Escudero, and Yoon (2001) point out that the standard specification tests, such as the Honda (1985) test, are not valid when they test for either cross-sectional random effects or serial correlation without considering the presence of the other effects. They suggested a modified Rao’s score (RS) test, which was further enhanced by Baltagi and Li (1991, 1995). You can obtain the modified Rao’s score test by specifying the BSY option. Baltagi and Li (1995) derived a two-sided LM test statistic for testing a white noise component in a fixed one-way model. You can request this test by specifying the BL95 option. Several tests are available to test first-order correlation in fixed-effects models. You can obtain these tests by specifying the DW, BW, or BFN option.