Data Requirements for 3-D Plots

Overview of the Data Requirements for 3-D Plots

Both of the plot statements that can be used in the OVERLAY3D layout are parameterized plots (see Plot Statement Terminology and Concepts). This means that the input data must conform to certain prerequisites in order for the plot to be drawn.

Parameterized plots do not perform any internal data transformations or computing for you. So, in most cases, you will need to perform some kind of preliminary data manipulation to set up the input data correctly before executing the template. The types of data transformations that you need to perform are commonly known as "binning" and "gridding."

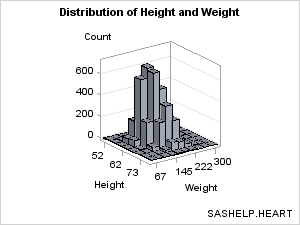
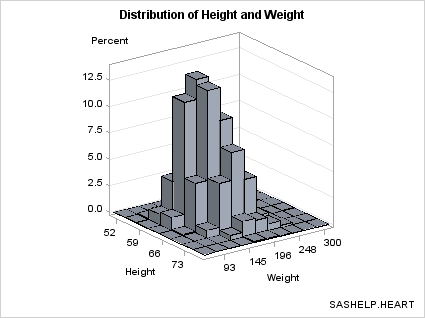
Producing Bivariate Histograms

A bivariate histogram shows the distribution of data for two continuous numeric variables. In the following graph, the X axis displays HEIGHT values and the Y axis displays WEIGHT values. The Z axis represents the frequency count of observations. The Z values could be some other measure (for example, percentage of observations), but they can never be negative.

Bivariate Histogram of Height and Weight

As with a standard histogram, the X and Y variables in the bivariate histogram have been uniformly binned, which means that their data ranges have been divided into equal sized intervals (bins), and that observations are distributed into one of these bin combinations.

The BIHISTOGRAM3DPARM statement, which produced this plot, does not perform any binning computation on the input columns. Thus, you must pre-bin the data. In the following example, the binning is done with PROC KDE (part of the SAS/STAT product).

proc kde data=sashelp.heart;
  bivar height(ngrid=8) weight(ngrid=10) /
        out=kde(keep=value1 value2 count) noprint plots=none;
run;

In this program, the NGRID= option sets the number of bins to create for each variable. The default for NGRID is 60. The binned values for HEIGHT are stored in VALUE1, and the binned values for WEIGHT are stored in VALUE2. This selection of bins produces 1 observation for each of the 80 bin combinations. Frequency counts for each bin combination are placed in a COUNT variable in the output data set.

Notice that when you form the grid by choosing the number of bins, the bin widths (about 3.5 for HEIGHT and about 26 for WEIGHT) are most often non-integer.

The following template definition displays this data. By default, the BINAXIS=TRUE setting requests that X and Y axes show tick values at bin boundaries. Also by default, XVALUES=MIDPOINTS and YVALUES=MIDPOINTS, which means that the X and Y columns represent midpoint values rather than lower bin boundaries (LEFTPOINTS) or upper bin boundaries (RIGHTPOINTS). Not all of the bins in this graph can be labelled without collision because the graph is small. Thus, the ticks and tick values were thinned. The non-integer bin values are converted to integers ( TICKVALUEFORMAT=5. ) to simplify the axis tick values. DISPLAY=ALL means "show outlined, filled bins."

proc template;
  define statgraph bihistogram1a;
    begingraph;
      entrytitle "Distribution of Height and Weight";
      entryfootnote halign=right "SASHELP.HEART";
      layout overlay3d / cube=false zaxisopts=(griddisplay=on)
          xaxisopts=(linearopts=(tickvalueformat=5.))
          yaxisopts=(linearopts=(tickvalueformat=5.));
        bihistogram3dparm x=value1 y=value2 z=count /
          display=all;
      endlayout;
    endgraph;
  end;
run;

proc sgrender data= kde template=bihistogram1a;
  label value1="Height" value2="Weight";
run;

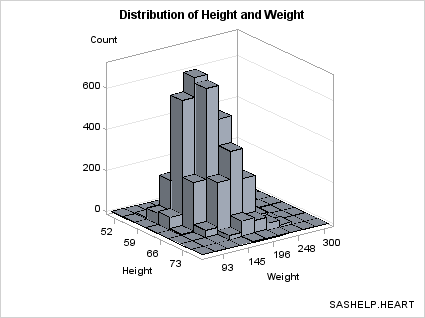
Bivariate Histogram Using the PROC KDE Output Data

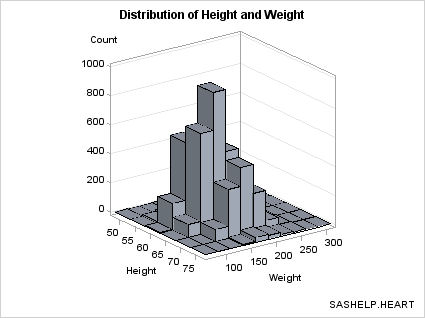
Eliminating Bins that Have No Data. Notice that the bins of 0 frequency (there are several) are included in the plot. If you want to eliminate the bins where there is no data, you can generate a subset of the data. The subset makes it a bit clearer where there are bins with small frequency counts verses portions of the grid with no data.

proc sgrender data= kde template=bihistogram1a;
  where count > 0;
  label value1="Height" value2="Weight";
run;

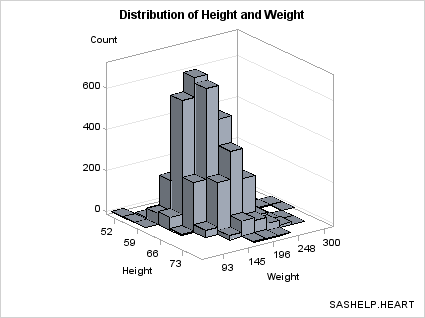
Bivariate Histogram Using a Subset of the Data

Displaying Percentages on Z Axis. To display the percentage of observations on the Z axis instead of the actual count, you need to perform an additional data transformation to convert the counts to percentages.

proc kde data=sashelp.heart;
  bivar height(ngrid=8) weight(ngrid=10) /
        out=kde(keep=value1 value2 count) noprint plots=none;
run;

data kde;
  if _n_ = 1 then do i=1 to rows;
    set kde(keep=count) point=i nobs=rows;
    TotalObs+count;
  end;
  set kde;
  Count=100*(Count/TotalObs);
  label Count="Percent";
run;

proc sgrender data= kde template=bihistogram1a;
   label value1="Height" value2="Weight";
run;

Bivariate Histogram Showing Percentages Rather Than Counts

Setting Bin Width. Another technique for binning data is to set a bin width and compute the number of observations in each bin. In the DATA step below, 5 is the bin width for HEIGHT and 25 for WEIGHT. With this technique you do not know the exact number of bins, but you can assure that the bins are of a "good" size.

data heart;
  set sashelp.heart(keep=height weight);
  if height ne . and weight ne .;
  height=round(height,5);
  weight=round(weight,25);
run;

After rounding, HEIGHT and WEIGHT can be used as classifiers for a summarization. Notice that the COMPLETETYPES option forces all possible combinations of the two variables to be output, even if no data exists for a particular crossing.

proc summary data=heart nway completetypes;
  class height weight;
  var height;
  output out=stats(keep=height weight count) N=Count;
run;

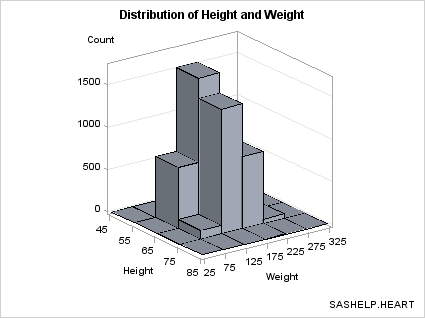
The template can be simplified because we know that the bin midpoints are uniformly spaced integers. For this selection of bin widths, 6 bins were produced for HEIGHT and 10 for WEIGHT.

proc template;
  define statgraph bihistogram2a;
    begingraph;
      entrytitle "Distribution of Height and Weight";
      entryfootnote halign=right "SASHELP.HEART";
      layout overlay3d / cube=false zaxisopts=(griddisplay=on);
        bihistogram3dparm x=height y=weight z=count /
          display=all;
      endlayout;
    endgraph;
  end;
run;

proc sgrender data=stats template=bihistogram2a;
run;

If you prefer to see the axes labeled with the bin endpoints rather the bin midpoints, you can use the ENDLABELS=TRUE setting on the BIHISTOGRAM3DPARM statement. Note that the ENDLABELS= option is independent of the XVALUES= and YVALUES= options.

In the following example, the bin widths are changed to even numbers (10 and 50) to make the bin endpoints even numbers:

proc template;
  define statgraph bihistogram2a;
    begingraph;
      entrytitle "Distribution of Height and Weight";
      entryfootnote halign=right "SASHELP.HEART";
      layout overlay3d / cube=false zaxisopts=(griddisplay=on);
        bihistogram3dparm x=height y=weight z=count /
          binaxis=true endlabels=true display=all;
      endlayout;
    endgraph;
  end;
run;
data heart;
  set sashelp.heart(keep=height weight);
  height=round(height,10);
  weight=round(weight,50);
run;
proc summary data=heart nway completetypes;
  class height weight;
  var height;
  output out=stats(keep=height weight count) N=Count;
run;

proc sgrender data=stats template=bihistogram2a;
run;

If you choose bin widths that are too small, "gaps" might be displayed among axis ticks values, which might cause the following message:

WARNING: The data for a HISTOGRAMPARM statement is not appropriate.
         HISTOGRAMPARM statement expects uniformly-binned data. The
         histogram might not be drawn correctly.

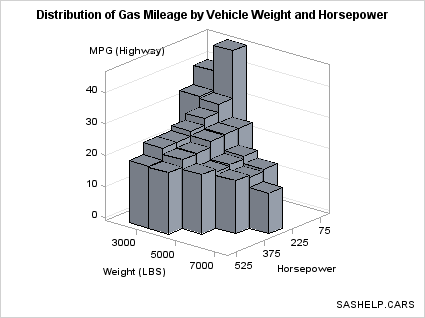
Because BIHISTOGRAM3DPARM is a parameterized plot, you can use it to show the 3-D data summarization of a response variable Z, which must have non-negative values, by two numeric classification variables that are uniformly spaced (X and Y). That is, even though the graphical representation is a bivariate histogram, the Z axis does not have to display a frequency count or a percent.

data cars;
  set sashelp.cars(keep=weight horsepower mpg_highway);
  if horsepower ne . and weight ne .;
  horsepower=round(horsepower,75);
  weight=round(weight,1000);
run;
 
proc summary data=cars nway completetypes;
  class weight horsepower;
  var mpg_highway;
  output out=stats mean=Mean ;
run;

proc template;
  define statgraph bihistogram2b;
    begingraph;
      entrytitle
       "Distribution of Gas Mileage by Vehicle Weight and Horsepower";
      entryfootnote halign=right "SASHELP.CARS";
      layout overlay3d / cube=false zaxisopts=(griddisplay=on) rotate=130;
        bihistogram3dparm y=weight x=horsepower z=mean / binaxis=true
          display=all;
      endlayout;
    endgraph;
  end;
run;

proc sgrender data=stats template=bihistogram2b;
run;

Bivariate Histogram with Z Axis Representing a Response Variable

Producing Surface Plots

A surface plot shows points that are defined by three continuous numeric variables and connected with a polygon mesh. A polygon mesh is a collection of vertices, edges, and faces that defines the shape of a polyhedral object, which simulates the surface. For a surface to be drawn, the input data must be "gridded"; that is, the X and Y data ranges are split into uniform intervals (the grid), and the corresponding Z values are computed for each X,Y pair. Smaller data grid intervals produce a smoother surface because more smaller polygons are used but are more resource intensive because of the large number of polygons that are generated. Larger data grid intervals produce a coarser, faceted surface because the polygon mesh has fewer faces and is less resource intensive.

The faces of the polygons can be filled, and lighting is applied to the polygon mesh to create the 3-D effect. It is possible to superimpose a grid on the surface. The grid display is a sampling of the data grid boundaries that intersect the surface. The grid display can be thought of as a simpler see-through line version of the surface and can be rendered with or without displaying the filled surface.

The default appearance of a surface is a filled polygon mesh with superimposed grid lines.

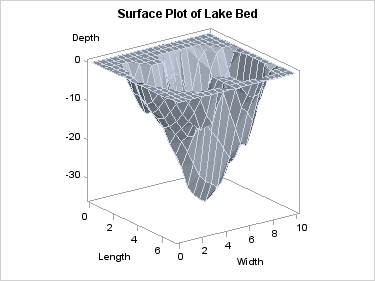
surfaceplotparm x=length y=width z=depth;

The SURFACEPLOTPARM statement assumes that the response/Z values have been provided for a uniform X-Y grid. Missing Z values will leave a "hole" in the surface.

The observations in the input data set should form an evenly spaced grid of horizontal (X and Y) values and one vertical (Z) value for each of these combinations. The observations should be in sorted order of Y and X to obtain an accurate graph. The sort direction for Y should be ascending. The sort direction of X can be either ascending or descending.

In the following example, 315 observations in SASHELP.LAKE are gridded into a 15 by 21 grid. The length of the grid is from 0 to 7 by .5, and the width of the grid is from 0 to 10 by .5 There are no missing Depth values.

Input data with non-gridded columns should be preprocessed with PROC G3GRID. This procedure creates an output data set, and it allows specification of the grid size and various methods for computed interpolated Z column(s). For further details, see the documentation for PROC G3GRID in the SAS/GRAPH: Reference.

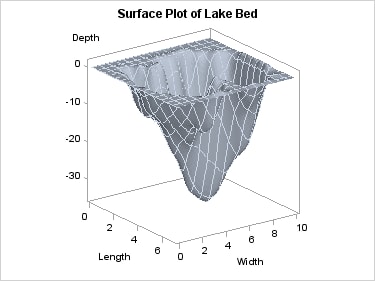
Using PROC G3GRID, the following code performs a Spline interpolation and generates a surface plot. By increasing the grid size and specifying a SPLINE interpolation, a smoother surface is rendered.

proc g3grid data=sashelp.lake out=spline;
  grid width*length = depth / naxis1=75 naxis2=75 spline;
run;

proc sgrender data=spline template=surfaceplotparm;
run;

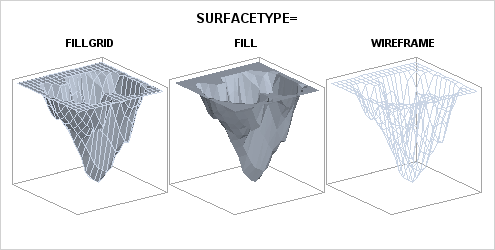
The SURFACETYPE= option offers three different types of surface rendering:

FILLGRID	a filled surface with grid outlines (the default)
FILL	a filled surface without grid outlines
WIREFRAME	an unfilled (see through) surface with grid outlines

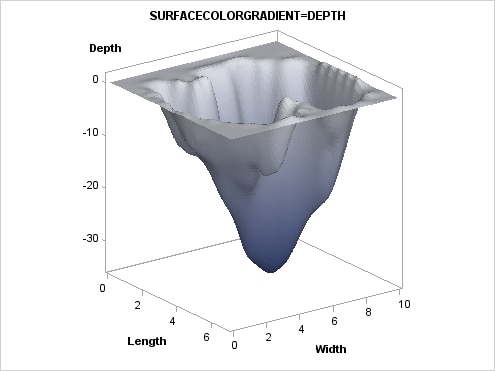
Adding a Color Gradient. The surface can be colored with a gradient that is based on a response variable by setting a column on the SURFACECOLORGRADIENT= option. The following example uses the DEPTH variable:

proc template;
  define statgraph surfaceplotparm;
    begingraph;
      entrytitle "SURFACECOLORGRADIENT=DEPTH";
      layout overlay3d / cube=false;
      surfaceplotparm x=length y=width z=depth /
        surfacetype=fill
        surfacecolorgradient=depth
        colormodel=twocolorramp
        reversecolormodel=true ;
      endlayout;
    endgraph;
  end;
run;

/* create gridded data for surface */
proc g3grid data=sashelp.lake out=spline;
  grid width*length = depth / naxis1=75 naxis2=75 spline;
run;
 
proc sgrender data=spline template=surfaceplotparm;
run;

The COLORMODEL=TWOCOLORRAMP setting indicates a style element. Four possible color ramps are supplied in every style. The REVERSECOLORMODEL=TRUE setting exchanges (reverses) the start color and end color that is defined by the color model. The colors were reversed so that the darker color maps to the lower depths.

Surface Plot with Two-color Ramp and Reversed Color Model

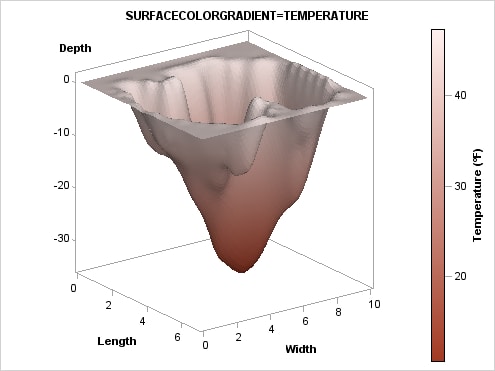
Using Color to Show an Additional Response Variable. The SURFACECOLORGRADIENT= option does not have to use the Z= variable. In the next example, another variable, TEMPERATURE is used. Notice that it is possible to display a continuous legend when you use the SURFACECOLORGRADIENT= option. Several legend options can be used. Using other color ramps and continuous legends are discussed in more detail in Adding Legends to a Graph.

ods escapechar="^"; /* Define an escape character */

proc template;
  define statgraph surfaceplot;
   begingraph;
     entrytitle "SURFACECOLORGRADIENT=TEMPERATURE";
     layout overlay3d / cube=false;
       surfaceplotparm x=length y=width z=depth / name="surf"
           surfacetype=fill 
           surfacecolorgradient=temperature
           reversecolormodel=true
           colormodel=twocoloraltramp ;
       continuouslegend "surf" /
           title="Temperature (^{unicode '00B0'x}F)" ;
     endlayout;
   endgraph;
  end;
run;
 
data lake;
  set sashelp.lake;
  if depth = 0 then Temperature=46;
  else Temperature=46+depth;
run;
 
/* create gridded data for surface */
proc g3grid data=lake out=spline;
   grid width*length = depth temperature / naxis1=75 naxis2=75 spline;
run;

proc sgrender data=spline template=surfaceplot;
run;