APPCORT Call
CALL APPCORT (prqb, lindep, a, b, <, sing> ) ;
If ![]() is rank-deficient, then the least squares problem
is rank-deficient, then the least squares problem ![]() has infinitely many solutions (Golub and Van Loan, 1989, p. 241). However, there is a unique solution which has the smallest Euclidean norm. The APPCORT subroutine computes the
minimum Euclidean-norm solution of the (rank-deficient) least squares problem by applyng a complete orthogonal decomposition
by Householder transformations to the vector
has infinitely many solutions (Golub and Van Loan, 1989, p. 241). However, there is a unique solution which has the smallest Euclidean norm. The APPCORT subroutine computes the
minimum Euclidean-norm solution of the (rank-deficient) least squares problem by applyng a complete orthogonal decomposition
by Householder transformations to the vector ![]() .
.
The input arguments to the APPCORT subroutine are as follows:
- a
-
is an
 matrix
matrix 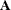 , with
, with 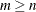 , which is to be decomposed into the product of the
, which is to be decomposed into the product of the  orthogonal matrix
orthogonal matrix 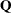 , the
, the 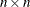 upper triangular matrix
upper triangular matrix 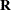 , and the
, and the 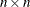 orthogonal matrix
orthogonal matrix 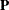 ,
,
![\[ \bA = \bQ \left[ \begin{array}{c} \bR \\ \mb {0} \end{array} \right] \bPi ^{\prime } \bP ^{\prime } \bPi \]](images/imlug_langref0060.png)
- b
-
is a
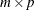 matrix,
matrix, 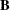 .
.
- sing
-
is an optional scalar that specifies a singularity criterion.
The APPCORT subroutine returns the following values:
- prqb
-
is an
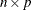 matrix product
matrix product
![\[ \bP \bPi \left[ \begin{array}{cc} (\bL ^{\prime })^{-1} & \mb {0} \\ \mb {0} & \mb {0} \end{array} \right] \bQ ^{\prime } \bB \]](images/imlug_langref0064.png)
which is the minimum Euclidean-norm solution of the rank-deficient least squares problem
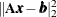 .
.
- lindep
-
is the number of linearly dependent columns in the matrix
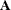 that are detected by applying the
that are detected by applying the  Householder transformations. That is, lindep is
Householder transformations. That is, lindep is  , where
, where  is the numerical rank of
is the numerical rank of 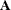 .
.
See the section COMPORT Call for information about complete orthogonal decomposition.
The following example uses the APPCORT call to solve a rank-deficient least squares problem:
/* compute solution for rank-deficient least squares problem:
min |Ax-b|^2
The range of A is a line; b is a point not on the line. */
A = {1 2,
2 4,
-1 -2};
b = {1, 3, -2};
call appcort(x,lindep,A,b);
print x;
Figure 23.38: Solution to a Rank-Deficient Least Squares Problem
| x |
|---|
| 0.3 |
| 0.6 |
The argument b can also be a matrix. If b is an identity matrix, then you can use the APPCORT subroutine to form a generalized inverse, as shown in the following example:
/* A has only four linearly independent columns */
A = {1 0 1 0 0,
1 0 0 1 0,
1 0 0 0 1,
0 1 1 0 0,
0 1 0 1 0,
0 1 0 0 1 };
/* compute Moore-Penrose generalized inverse */
b = i(nrow(A)); /* identity matrix */
call appcort(Ainv, lindep, A, b);
print Ainv;
/* verify generalized inverse conditions (Golub & Van Loan, p. 243) */
eps = 1e-12;
if any(A*Ainv*A-A > eps) |
any(Ainv*A*Ainv-Ainv > eps) |
any((A*Ainv)`-A*Ainv > eps) |
any((Ainv*A)`-Ainv*A > eps) then
msg = "Pseudoinverse conditions not satisfied";
else
msg = "Pseudoinverse conditions satisfied";
print msg;
Figure 23.39: Generalized Inverse
| Ainv | |||||
|---|---|---|---|---|---|
| 0.2666667 | 0.2666667 | 0.2666667 | -0.066667 | -0.066667 | -0.066667 |
| -0.066667 | -0.066667 | -0.066667 | 0.2666667 | 0.2666667 | 0.2666667 |
| 0.4 | -0.1 | -0.1 | 0.4 | -0.1 | -0.1 |
| -0.1 | 0.4 | -0.1 | -0.1 | 0.4 | -0.1 |
| -0.1 | -0.1 | 0.4 | -0.1 | -0.1 | 0.4 |
| msg |
|---|
| Pseudoinverse conditions satisfied |