DISTANCE Function
DISTANCE (x, <, method> ) ;
The DISTANCE function computes the pairwise distances between rows of x. The distances depend on the metric specified by the method argument. The arguments are as follows:
- x
-
specifies an
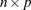 numerical matrix that contains
numerical matrix that contains  points in
points in 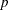 -dimensional space.
-dimensional space.
- method
-
is an optional argument that specifies the method used to specify the distance between pairs of points. The method argument is either a numeric value, method
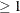 , or a case-insensitive character value. Only the first four character values are used. The following are valid options:
, or a case-insensitive character value. Only the first four character values are used. The following are valid options:
- “L2”
-
specifies that the function compute the Euclidean (
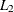 ) distance between two points. This is the default value. An equivalent alias is “Euclidean”.
) distance between two points. This is the default value. An equivalent alias is “Euclidean”.
- “L1”
-
specifies that the function compute the Manhattan (
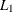 ) distance between two points. An equivalent alias is “CityBlock” or “Manhattan”.
) distance between two points. An equivalent alias is “CityBlock” or “Manhattan”.
- “LInf”
-
specifies that the function compute the Chebyshev (
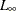 ) distance between two points. An equivalent alias is “Chebyshev”.
) distance between two points. An equivalent alias is “Chebyshev”.
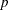
-
is a numeric value,
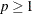 , that specifies the
, that specifies the 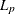 -norm.
-norm.
The DISTANCE function returns an ![]() symmetric matrix. The
symmetric matrix. The ![]() th element is the distance between the
th element is the distance between the ![]() th and
th and ![]() th rows of x.
th rows of x.
If ![]() and
and ![]() are two
are two ![]() -dimensional points, then the following formulas are used to compute the distance between
-dimensional points, then the following formulas are used to compute the distance between ![]() and
and ![]() :
:
-
The Euclidean distance:
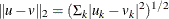 .
.
-
The
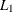 distance:
distance: 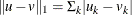 ,
,
-
The
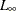 distance:
distance: 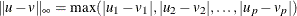 .
.
-
The
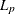 distance:
distance: 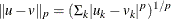 .
.
The following statements illustrate the DISTANCE function:
x = {1 0,
0 1,
-1 0,
0 -1};
d2 = distance(x, "L2");
print d2[format=best5.];
Figure 23.93: Euclidean Distance Between Pairs of Points
| d2 | |||
|---|---|---|---|
| 0 | 1.414 | 2 | 1.414 |
| 1.414 | 0 | 1.414 | 2 |
| 2 | 1.414 | 0 | 1.414 |
| 1.414 | 2 | 1.414 | 0 |
The ![]() th column of
th column of d2 contains the distances between the ![]() th row of
th row of x and the other rows. Notice that the d2 matrix has zeros along the diagonal.
You can also compute non-Euclidean distances, as follows:
d1 = distance(x, "L1"); dInf = distance(x, "LInfinity"); print d1, dInf;
Figure 23.94: Distance Between Pairs of Points
| d1 | |||
|---|---|---|---|
| 0 | 2 | 2 | 2 |
| 2 | 0 | 2 | 2 |
| 2 | 2 | 0 | 2 |
| 2 | 2 | 2 | 0 |
| dInf | |||
|---|---|---|---|
| 0 | 1 | 2 | 1 |
| 1 | 0 | 1 | 2 |
| 2 | 1 | 0 | 1 |
| 1 | 2 | 1 | 0 |
If a row contains a missing value, all distances that involve that row are assigned a missing value.