FARMALIK Call :: SAS/IML(R) 12.1 User's Guide

FARMALIK Call

CALL FARMALIK (lnl, series, d <*>, phi <*>, theta <*>, sigma <*>, p <*>, q <*>, opt ) ;

The FARMALIK subroutine evaluates the log-likelihood function of an ARFIMA() model for a given time series.

The input arguments to the FARMALIK subroutine are as follows:

series

specifies a time series (assuming mean zero).

d

specifies a fractional differencing order. This argument is required; the value of 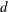should be in the open interval 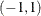excluding zero.

phi

specifies an 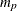-dimensional vector that contains the autoregressive coefficients, where 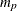is the number of the elements in the subset of the AR order. The default is zero.

theta

specifies an 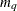-dimensional vector that contains the moving average coefficients, where 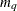is the number of the elements in the subset of the MA order. The default is zero.

sigma

specifies a variance of the innovation series. The default is one.

p

specifies the subset of the AR order. See the FARMACOV subroutine for additional details.

q

specifies the subset of the MA order. See the FARMACOV subroutine for additional details.

opt

specifies the method of computing the log-likelihood function. The following are valid values:

0: requests the conditional sum of squares function. This is the default.
1: requests the exact log-likelihood function. This option requires that the time series be stationary and invertible.

The FARMALIK subroutine returns the following value:

lnl: is a three-dimensional vector. If opt 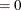is specified, the conditional sum of squares function is evaluated and the result returns in lnl[1]. Otherwise, lnl[1] contains the log-likelihood function of the model; lnl[2] contains the sum of the log determinant of the innovation variance; and lnl[3] contains the weighted sum of squares of residuals. The log-likelihood function is computed as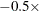 $-0.5\times$ (lnl[2]+lnl[3]).

As an example, consider the following ARFIMA() model:

$(1-0.5B)(1-B)^{0.3}y_ t = (1+0.1B){\epsilon }_ t$

In this model, ${\epsilon }_ t \sim NID(0,1.2)$ . The following statements compute the log-likelihood function of this model:

d = 0.3;
phi = 0.5;
theta = -0.1;
sigma = 1.2;
call farmasim(yt, d, phi, theta, sigma) seed=1234;
call farmalik(lnl, yt, d, phi, theta, sigma);
print (lnl[1])[label="Conditional Sum of Squares"];

Figure 23.115: Log-Likelihood for an ARFIMA Model

Conditional Sum of Squares
-16.67587

The FARMALIK subroutine computes a log-likelihood function of the ARFIMA() model. The exact log-likelihood function was proposed by Sowell (1992); the conditional sum of squares function was proposed by Chung (1996).

The exact log-likelihood function only considers a stationary and invertible ARFIMA() process with $d\in (-0.5,0.5)\backslash \{ 0\}$ represented as

$\phi (B)(1-B)^ dy_ t = \theta (B){\epsilon }_ t$

where ${\epsilon }_ t \sim NID(0,\sigma ^2)$ .

Let $Y_ T=\left[y_1,y_2,\ldots ,y_ T \right]’$ and the log-likelihood function is as follows without a constant term:

$\ell = -{1 \over 2} (\log |\Sigma | + Y_ T’\Sigma ^{-1}Y_ T )$

where $\Sigma = \left[ \gamma _{i-j} \right]$ for $i,j=1,2,\ldots ,T$ .

The conditional sum of squares function does not require the normality assumption. The initial observations , $y_{-1}, \ldots$ and ${\epsilon }_0$ , ${\epsilon }_{-1}, \ldots$ are set to zero.

Let be an ARFIMA() process represented as

$\phi (B)(1-B)^ dy_ t = \theta (B){\epsilon }_ t$

Then the conditional sum of squares function is

$\ell = -{T \over 2}\log \left( {1 \over T}\sum _{t=1}^ T{\epsilon }_ t^2 \right)$