FDIF Call
CALL FDIF (out, series, d) ;
The FDIF subroutine computes a fractionally differenced process. The input arguments to the FDIF subroutine are as follows:
- series
-
specifies a time series with
 length.
length.
- d
-
specifies a fractional differencing order. This argument is required; the value of
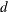 should be in the open interval
should be in the open interval 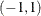 excluding zero.
excluding zero.
The FDIF subroutine returns the following value:
- out
-
is an
 vector that contains the fractionally differenced process.
vector that contains the fractionally differenced process.
As an example, consider an ARFIMA(![]() ) process
) process
|
|
Let ![]() ; that is,
; that is, ![]() follows an ARMA(1,1). The following statements compute the filtered series
follows an ARMA(1,1). The following statements compute the filtered series ![]() :
:
d = 0.3; phi = 0.5; theta = -0.1; call farmasim(yt, d, phi, theta) n=10 seed=1234; call fdif(zt, yt, d); print zt;
Figure 23.117: A Fractionally Differenced Process
| zt |
|---|
| . |
| 3.0146839 |
| 4.0190575 |
| 3.3402864 |
| -0.41881 |
| 1.6149336 |
| 1.1998534 |
| -0.137789 |
| -1.475051 |
| -1.670366 |