FULL Function
FULL (x <, nrow> <, ncol> ) ;
The FULL function converts a matrix stored in a sparse format into a matrix stored in a dense format. See the SPARSE function for a description of how sparse matrices are stored.
The arguments are as follows:
- x
-
specifies a
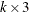 numerical matrix that contains a sparse representation of an
numerical matrix that contains a sparse representation of an 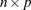 matrix.
matrix.
- nrow
-
specifies the number of rows in the dense matrix. If this argument is not specified, then the number of rows is determined by the maximum value of the second column of x.
- ncol
-
specifies the number of columns in the dense matrix. If this argument is not specified, then the number of columns is determined by the maximum value of the third column of x.
The matrix returned by the FULL function is an ![]() matrix with
matrix with ![]() nonzero values determined by the x matrix, as shown in the following example:
nonzero values determined by the x matrix, as shown in the following example:
s = {3 1 1,
1.1 2 1,
4 2 2,
1 3 2,
10 3 3,
3.2 4 2,
3 4 4 };
x = full(s);
print x;
Figure 23.123: Matrix Converted from Sparse to Dense Storage
| x | |||
|---|---|---|---|
| 3 | 0 | 0 | 0 |
| 1.1 | 4 | 0 | 0 |
| 0 | 1 | 10 | 0 |
| 0 | 3.2 | 0 | 3 |
In the previous example, the s matrix specifies a lower triangular matrix. However, the s matrix might represent a symmetric matrix rather than a lower triangular matrix, but only the lower triangular entries were
stored. (For example, the s matrix might have been created by the SPARSE function by using the “SYM” option; see the SPARSE function documentation.) If that is the case, you can use the following statement to recover the symmetric matrix representation of
s:
xSym = (x+x`)- diag(x); print xSym;
Figure 23.124: Symmetric Matrix Converted from Sparse Symmetric Storage
| xSym | |||
|---|---|---|---|
| 3 | 1.1 | 0 | 0 |
| 1.1 | 4 | 1 | 3.2 |
| 0 | 1 | 10 | 0 |
| 0 | 3.2 | 0 | 3 |
By default, the size of the matrix returned by the FULL function is determined by the maximum row and column entry in the first argument. You can override this behavior by specifying values for the number of rows and columns returned by the FULL function, as shown in the following statements:
z = full(s, 5, 6); print z;
Figure 23.125: Matrix with Zeros in Last Row or Column
| z | |||||
|---|---|---|---|---|---|
| 3 | 0 | 0 | 0 | 0 | 0 |
| 1.1 | 4 | 0 | 0 | 0 | 0 |
| 0 | 1 | 10 | 0 | 0 | 0 |
| 0 | 3.2 | 0 | 3 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 |