GSORTH Call :: SAS/IML(R) 12.1 User's Guide

GSORTH Call

CALL GSORTH (P, T, lindep, A) ;

The GSORTH subroutine computes the Gram-Schmidt orthonormal factorization of the $m \times n$ matrix $\mb {A}$ , where is greater than or equal to . The GSORTH subroutine implements an algorithm described by Golub (1969).

The GSORTH subroutine has a single input argument:

A: is an input $m \times n$ matrix.

The output arguments to the GSORTH subroutine are as follows:

P: is an $m \times n$ column-orthonormal output matrix.
T: is an upper triangular 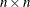$n \times n$ output matrix.
lindep: is a flag with a value of 0 if columns of A are independent and a value of 1 if they are dependent. The lindep argument is an output scalar.

Specifically, the GSORTH subroutine computes the column-orthonormal $m \times n$ matrix $\mb {P}$ and the upper triangular $n \times n$ matrix $\mb {T}$ such that

$\mb {A}= \mb {P}*\mb {T}$

If the columns of $\mb {A}$ are linearly independent (that is, rank $(\mb {A})=n$ ), then $\mb {P}$ is full-rank column-orthonormal: $\mb {P}^{\prime }\mb {P}=\mb {I}_ w$ , $\mb {T}$ is nonsingular, and the value of lindep (a scalar) is set to 0. If the columns of $\mb {A}$ are linearly dependent (say, rank $(\mb {A})=k < n$ ) then columns of $\mb {P}$ are set to 0, the corresponding rows of $\mb {T}$ are set to 0 ( $\mb {T}$ is singular), and lindep is set to 1. The pattern of zero columns in $\mb {P}$ corresponds to the pattern of linear dependencies of the columns of $\mb {A}$ when columns are considered in left-to-right order.

The following statements call the GSORTH subroutine and print the output parameters to the call:

x = {1 1 3 1 2,
     1 0 1 2 3,
     1 1 3 3 4,
     1 0 1 4 5,
     1 1 3 5 6,
     1 0 1 6 7};
call gsorth(P, T, lindep, x);
reset fuzz;
print P, T, lindep;

Figure 23.133: Results of a Gram-Schmidt Orthonormalization

P
0.4082483	0.4082483	-0.5
0.4082483	-0.408248	-0.5
0.4082483	0.4082483	0
0.4082483	-0.408248	0
0.4082483	0.4082483	0.5
0.4082483	-0.408248	0.5

T
2.4494897	1.2247449	4.8989795	8.5732141	11.022704
0	1.2247449	2.4494897	-1.224745	-1.224745
0	0	0	0	0
0	0	0	4	4
0	0	0	0	0

lindep
1

If lindep is 1, you can permute the columns of $\mb {P}$ and rows of $\mb {T}$ so that the zero columns of $\mb {P}$ are rightmost—that is, $\mb {P}=(\mb {P}_1,\ldots ,\mb {P}_,k,0,\ldots ,0)$ , where is the column rank of $\mb {A}$ and the equality $\mb {A}=\mb {P}*\mb {T}$ is preserved. The following statements show a permutation of columns:

d = loc(vecdiag(T)^=0) || loc(vecdiag(T)=0);
temp = P;
P[,d] = temp;
temp = T;
T[,d] = temp;
print d, P, T;

Figure 23.134: Rearranging Columns

d
1	2	4	3	5

P
0.4082483	0.4082483	-0.5
0.4082483	-0.408248	-0.5
0.4082483	0.4082483	0
0.4082483	-0.408248	0
0.4082483	0.4082483	0.5
0.4082483	-0.408248	0.5

T
2.4494897	1.2247449	8.5732141	4.8989795	11.022704
0	1.2247449	-1.224745	2.4494897	-1.224745
0	0	0	0	0
0	0	4	0	4
0	0	0	0	0

The GSORTH subroutine is not recommended for the construction of matrices of values of orthogonal polynomials; the ORPOL function should be used for that purpose.