KALCVF Call :: SAS/IML(R) 12.1 User's Guide

KALCVF Call

CALL KALCVF (pred, vpred, filt, vfilt, data, lead, a, f, b, h, var <*>, z0 <*>, vz0 ) ;

The KALCVF subroutine computes the one-step prediction $z_{t+1|t}$ and the filtered estimate $z_{t|t}$ , in addition to their covariance matrices. The call uses forward recursions, and you can also use it to obtain -step estimates.

The input arguments to the KALCVF subroutine are as follows:

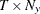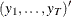data: is a $T \times N_ y$ matrix that contains data $(y_1, \ldots , y_ T)^{\prime }$ .
lead: is the number of steps to forecast after the end of the data.
a: is an 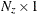$N_ z \times 1$ vector for a time-invariant input vector in the transition equation, or a 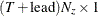$(T+\mbox{lead})N_ z \times 1$ vector that contains input vectors in the transition equation.
f: is an 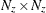$N_ z \times N_ z$ matrix for a time-invariant transition matrix in the transition equation, or a 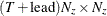$(T+\mbox{lead})N_ z \times N_ z$ matrix that contains transition matrices in the transition equation.
b: is an 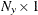$N_ y \times 1$ vector for a time-invariant input vector in the measurement equation, or a 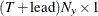$(T+\mbox{lead})N_ y \times 1$ vector that contains input vectors in the measurement equation.
h: is an 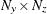$N_ y \times N_ z$ matrix for a time-invariant measurement matrix in the measurement equation, or a 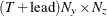$(T+\mbox{lead})N_ y \times N_ z$ matrix that contains measurement matrices in the measurement equation.
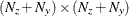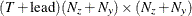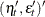var: is an $(N_ z + N_ y) \times (N_ z + N_ y)$ matrix for a time-invariant variance matrix for the error in the transition equation and the error in the measurement equation, or a $(T+\mbox{lead})(N_ z + N_ y) \times (N_ z + N_ y)$ matrix that contains variance matrices for the error in the transition equation and the error in the measurement equation—that is, $(\eta ^{\prime }_ t, \epsilon ^{\prime }_ t)^{\prime }$ .
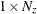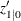z0: is an optional $1 \times N_ z$ initial state vector $z^{\prime }_{1|0}$ .
vz0: is an optional 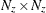$N_ z \times N_ z$ covariance matrix of an initial state vector $P_{1|0}$ .

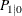The KALCVF call returns the following values:

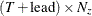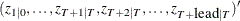pred: is a $(T+\mbox{lead}) \times N_ z$ matrix that contains one-step predicted state vectors $(z_{1|0},\ldots , z_{T+1|T}, z_{T+2|T}, \ldots , z_{T+\mbox{lead}|T})^{\prime }$ .
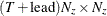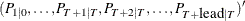vpred: is a $(T+\mbox{lead})N_ z \times N_ z$ matrix that contains mean square errors of predicted state vectors $(P_{1|0}, \ldots , P_{T+1|T}, P_{T+2|T}, \ldots , P_{T+\mbox{lead}|T})^{\prime }$ .
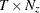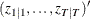filt: is a $T \times N_ z$ matrix that contains filtered state vectors $(z_{1|1}, \ldots , z_{T|T})^{\prime }$ .
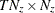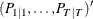vfilt: is a $TN_ z \times N_ z$ matrix that contains mean square errors of filtered state vectors $(P_{1|1}, \ldots , P_{T|T})^{\prime }$ .

The KALCVF call computes the conditional expectation of the state vector given the observations, assuming that the mean and the variance of the initial state vector are known. The filtered value is the conditional expectation of the state vector given the observations up to time . For -step forecasting where , the conditional expectation at time is computed given observations up to . For notation, and are variances of $\eta _ t$ and $\epsilon _ t$ , respectively, and is a covariance of $\eta _ t$ and $\epsilon _ t$ , and stands for the generalized inverse of . The filtered value and its covariance matrix are denoted $z_{t|t}$ and $P_{t|t}$ , respectively. For , $z_{t+k|t}$ and $P_{t+k|t}$ stand for the -step forecast of $z_{t+k}$ and its mean square error. The Kalman filtering algorithm for one-step prediction and filtering is given as follows:

$\displaystyle \hat{\epsilon }_ t$	$\displaystyle =$	$\displaystyle y_ t - b_ t - H_ t z_{t\|t-1}$
$\displaystyle D_ t$	$\displaystyle =$	$\displaystyle H_ t P_{t\|t-1} H^{\prime }_ t + R_ t$
$\displaystyle z_{t\|t}$	$\displaystyle =$	$\displaystyle z_{t\|t-1} + P_{t\|t-1} H^{\prime }_ t D_ t^- \hat{\epsilon }_ t$
$\displaystyle P_{t\|t}$	$\displaystyle =$	$\displaystyle P_{t\|t-1} - P_{t\|t-1} H^{\prime }_ t D_ t^- H_ t P_{t\|t-1}$
$\displaystyle K_ t$	$\displaystyle =$	$\displaystyle (F_ t P_{t\|t-1} H^{\prime }_ t + G_ t) D_ t^-$
$\displaystyle z_{t+1\|t}$	$\displaystyle =$	$\displaystyle a_ t + F_ t z_{t\|t-1} + K_ t \hat{\epsilon }_ t$
$\displaystyle P_{t+1\|t}$	$\displaystyle =$	$\displaystyle F_ t P_{t\|t-1}F^{\prime }_ t + V_ t - K_ t D_ t K^{\prime }_ t$

And for -step forecasting for ,

$\displaystyle z_{t+k\|t}$	$\displaystyle =$	$\displaystyle a_{t+k-1} + F_{t+k-1} z_{t+k-1\|t}$
$\displaystyle P_{t+k\|t}$	$\displaystyle =$	$\displaystyle F_{t+k-1} P_{t+k-1\|t} F^{\prime }_{t+k-1} + V_{t+k-1}$

When you use the alternative transition equation

$z_ t = a_ t + F_ t z_{t-1} + \eta _ t$

the forward recursion algorithm is written

$\displaystyle \hat{\epsilon }_ t$	$\displaystyle =$	$\displaystyle y_ t - b_ t - H_ t z_{t\|t-1}$
$\displaystyle D_ t$	$\displaystyle =$	$\displaystyle H_ t P_{t\|t-1} H^{\prime }_ t + H_ t \bG _ t + G^{\prime }_ t H^{\prime }_ t + \bR _ t$
$\displaystyle z_{t\|t}$	$\displaystyle =$	$\displaystyle z_{t\|t-1} + (P_{t\|t-1} H^{\prime }_ t + G_ t) D_ t^- \hat{\epsilon }_ t$
$\displaystyle P_{t\|t}$	$\displaystyle =$	$\displaystyle P_{t\|t-1} - (P_{t\|t-1} H^{\prime }_ t + G_ t) D_ t^- (H_ t P_{t\|t-1} + G^{\prime }_ t)$
$\displaystyle K_ t$	$\displaystyle =$	$\displaystyle (F_{t+1} P_{t\|t-1} H^{\prime }_ t + G_ t)D_ t^-$
$\displaystyle z_{t+1\|t}$	$\displaystyle =$	$\displaystyle a_{t+1} + F_{t+1} z_{t\|t-1} + K_ t \hat{\epsilon }_ t$
$\displaystyle P_{t+1\|t}$	$\displaystyle =$	$\displaystyle F_{t+1} P_{t\|t-1}F^{\prime }_{t+1} + V_{t+1} - K_ t D_ t K^{\prime }_ t$

And for -step forecasting ,

$\displaystyle z_{t+k\|t}$	$\displaystyle =$	$\displaystyle a_{t+k} + F_{t+k}z_{t+k-1\|t}$
$\displaystyle P_{t+k\|t}$	$\displaystyle =$	$\displaystyle F_{t+k} P_{t+k-1\|t} F^{\prime }_{t+k} + V_{t+k}$

You can use the KALCVF call when you specify the alternative transition equation and $\mathbf{G}_ t = \mb {0}$ .

The initial state vector and its covariance matrix of the time-invariant Kalman filters are computed under the stationarity condition

$\displaystyle z_{1\|0}$	$\displaystyle =$	$\displaystyle (I - F)^- a$
$\displaystyle P_{1\|0}$	$\displaystyle =$	$\displaystyle (I - F \otimes F)^- \mbox{vec}(V)$

where and are the time-invariant transition matrix and the covariance matrix of transition equation noise, and vec is an $N_ z^2 \times 1$ column vector that is constructed by the stacking columns of matrix . Note that all eigenvalues of the matrix are inside the unit circle when the SSM is stationary. When the preceding formula cannot be applied, the initial state vector estimate $z_{1|0}$ is set to and its covariance matrix $P_{1|0}$ is given by I. Optionally, you can specify initial values.

The KALCVF call accepts missing values in observations. If there is a missing observation, the filtered state vector for the missing observation is given by the one-step forecast.

The following program gives an example of the KALCVF call:

q = 2;
p = 2;
n = 10;
lead = 3;
total = n + lead;

seed = 25735;
x = round(10*normal(j(n, p, seed)))/10;
f = round(10*normal(j(q*total, q, seed)))/10;
a = round(10*normal(j(total*q, 1, seed)))/10;
h = round(10*normal(j(p*total, q, seed)))/10;
b = round(10*normal(j(p*total, 1, seed)))/10;

do i = 1 to total;
   temp = round(10*normal(j(p+q, p+q, seed)))/10;
   var = var//(temp*temp`);
end;

call kalcvf(pred, vpred, filt, vfilt, x, lead, a, f, b, h, var);

/* default initial state and covariance */
call kalcvs(sm, vsm, x, a, f, b, h, var, pred, vpred);
print sm[format=9.4] vsm[format=9.4];

Figure 23.158: Smoothed Estimate and Covariance

sm		vsm
-1.5236	-0.1000	1.5813	-0.4779
0.3058	-0.1131	-0.4779	0.3963
-0.2593	0.2496	2.4629	0.2426
-0.5533	0.0332	0.2426	0.0944
-0.5813	0.1251	0.2023	-0.0228
-0.3017	0.7480	-0.0228	0.5799
1.1333	-0.2144	0.8615	-0.7653
1.5193	-0.6237	-0.7653	1.2334
-0.6641	-0.7770	1.0836	0.8706
0.5994	2.3333	0.8706	1.5252
		0.3677	0.2510
		0.2510	0.2051
		0.3243	-0.4093
		-0.4093	1.2287
		0.1736	-0.0712
		-0.0712	0.9048
		1.3153	0.8748
		0.8748	1.6575
		8.6650	0.1841
		0.1841	4.4770

$\displaystyle \hat{\epsilon }_ t$	$\displaystyle =$	$\displaystyle y_ t - b_ t - H_ t z_{t\|t-1}$
$\displaystyle D_ t$	$\displaystyle =$	$\displaystyle H_ t P_{t\|t-1} H^{\prime }_ t + R_ t$
$\displaystyle z_{t\|t}$	$\displaystyle =$	$\displaystyle z_{t\|t-1} + P_{t\|t-1} H^{\prime }_ t D_ t^- \hat{\epsilon }_ t$
$\displaystyle P_{t\|t}$	$\displaystyle =$	$\displaystyle P_{t\|t-1} - P_{t\|t-1} H^{\prime }_ t D_ t^- H_ t P_{t\|t-1}$
$\displaystyle K_ t$	$\displaystyle =$	$\displaystyle (F_ t P_{t\|t-1} H^{\prime }_ t + G_ t) D_ t^-$
$\displaystyle z_{t+1\|t}$	$\displaystyle =$	$\displaystyle a_ t + F_ t z_{t\|t-1} + K_ t \hat{\epsilon }_ t$
$\displaystyle P_{t+1\|t}$	$\displaystyle =$	$\displaystyle F_ t P_{t\|t-1}F^{\prime }_ t + V_ t - K_ t D_ t K^{\prime }_ t$

$\displaystyle z_{t+k\|t}$	$\displaystyle =$	$\displaystyle a_{t+k-1} + F_{t+k-1} z_{t+k-1\|t}$
$\displaystyle P_{t+k\|t}$	$\displaystyle =$	$\displaystyle F_{t+k-1} P_{t+k-1\|t} F^{\prime }_{t+k-1} + V_{t+k-1}$

$\displaystyle \hat{\epsilon }_ t$	$\displaystyle =$	$\displaystyle y_ t - b_ t - H_ t z_{t\|t-1}$
$\displaystyle D_ t$	$\displaystyle =$	$\displaystyle H_ t P_{t\|t-1} H^{\prime }_ t + H_ t \bG _ t + G^{\prime }_ t H^{\prime }_ t + \bR _ t$
$\displaystyle z_{t\|t}$	$\displaystyle =$	$\displaystyle z_{t\|t-1} + (P_{t\|t-1} H^{\prime }_ t + G_ t) D_ t^- \hat{\epsilon }_ t$
$\displaystyle P_{t\|t}$	$\displaystyle =$	$\displaystyle P_{t\|t-1} - (P_{t\|t-1} H^{\prime }_ t + G_ t) D_ t^- (H_ t P_{t\|t-1} + G^{\prime }_ t)$
$\displaystyle K_ t$	$\displaystyle =$	$\displaystyle (F_{t+1} P_{t\|t-1} H^{\prime }_ t + G_ t)D_ t^-$
$\displaystyle z_{t+1\|t}$	$\displaystyle =$	$\displaystyle a_{t+1} + F_{t+1} z_{t\|t-1} + K_ t \hat{\epsilon }_ t$
$\displaystyle P_{t+1\|t}$	$\displaystyle =$	$\displaystyle F_{t+1} P_{t\|t-1}F^{\prime }_{t+1} + V_{t+1} - K_ t D_ t K^{\prime }_ t$

$\displaystyle z_{t+k\|t}$	$\displaystyle =$	$\displaystyle a_{t+k} + F_{t+k}z_{t+k-1\|t}$
$\displaystyle P_{t+k\|t}$	$\displaystyle =$	$\displaystyle F_{t+k} P_{t+k-1\|t} F^{\prime }_{t+k} + V_{t+k}$