LP Call :: SAS/IML(R) 12.1 User's Guide

Previous Page|Next Page

LP Call

CALL LP (rc, x, dual, a, b <*>, cntl <*>, u <*>, l <*>, basis ) ;

The LP subroutine solves the linear programming problem.

The input arguments to the LP subroutine are as follows:

a

is an $m \times n$ vector that specifies the technological coefficients, where 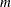is less than or equal to .

b

is an 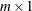$m \times 1$ vector that specifies the right-side vector.

cntl

is an optional row vector with one to five elements. If cntl=(indx, nprimal, ndual, epsilon, infinity), then

indx: is the subscript of nonzero objective coefficient.
nprimal: is the maximum number of primal iterations.
ndual: is the maximum number of dual iterations.
epsilon: is the value of virtual zero.
infinity: is the value of virtual infinity.

The default values are as follows: indx equals , nprimal equals 999,999, ndual equals 999,999, epsilon equals 1.0E8, and infinity is machine-dependent. If you specify ndual or nprimal or both, then on return they contain the number of iterations actually performed.

u

is an optional array of dimension that specifies upper bounds on the decision variables. If you do not specify u, the upper bounds are assumed to be infinity.

l

is an optional array of dimension that specifies lower bounds on the decision variables. If l is not given, then the lower bounds are assumed to be 0 for all the decision variables. This includes the decision variable associated with the objective value, which is specified by the value of indx.

basis

is an optional array of dimension that specifies the current basis. This is given by identifying which columns are explicitly in the basis and which columns are at their upper bound, as given in u. The absolute value of the elements in this vector is a permutation of the column indices. The columns specified in the first 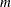elements of basis are considered the explicit basis. The absolute value of the last 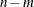elements of basis are the indices of the nonbasic variables. Any of the last 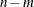elements of basis that are negative indicate that the corresponding nonbasic variable is at its upper bound. On return from the LP subroutine, the basis vector contains the final basis encountered. 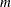If you do not specify basis, then the subroutine assumes that an initial basis is in the last columns of 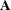$\mb {A}$ and that no nonbasic variables are at their upper bound.

rc

returns one of the following scalar return codes:

rc	Termination
0	The solution is optimal.
1	The solution is primal infeasible and dual feasible.
2	The solution is dual infeasible and primal feasible.
3	The solution is neither primal nor dual feasible.
4	A singular basis was encountered.
5	The solution is numerically unstable.
6	The subroutine could not obtain enough memory.
7	The number of iterations was exceeded.

x

returns the current primal solution in a column vector of length .

dual

returns the current dual solution in a row vector of length .

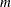The LP subroutine solves the linear program:

$\displaystyle$	$\displaystyle$	$\displaystyle \max (0,\ldots ,0,1,0,\ldots ,0) \mb {x}$
$\displaystyle$	$\displaystyle$	$\displaystyle \mbox{st. } \mb {Ax} = \mb {b}$
$\displaystyle$	$\displaystyle$	$\displaystyle l \leq \mb {x} \leq \mb {u}$

The subroutine first inverts the initial basis. If the basis vector is given, then the initial basis is the $m \times m$ submatrix identified by the first elements in basis; otherwise, the initial basis is defined by the last columns of $\mb {A}$ . If the initial basis is singular, the subroutine returns with RC=4. If the basis is nonsingular, then the current dual and primal solutions are evaluated. If neither is feasible, then the subroutine returns with RC=3. If the primal solution is feasible, then the primal algorithm iterates until either a dual feasible solution is encountered or the number of NPRIMAL iterations is exceeded. If the dual solution is feasible, then the dual algorithm iterates until either a primal feasible solution is encountered or the number of NDUAL iterations is exceeded. When a basis is identified that is both primal and dual feasible, then the subroutine returns with RC=0.

Care must be taken when solving a sequence of linear programs that use the NPRIMAL or NDUAL control parameters. Because the LP subroutine resets the NPRIMAL and NDUAL parameters to reflect the number of iterations executed, subsequent invocations of the LP subroutine will have the number of iterations limited to the number used by the last LP subroutine executed. In these cases you should consider resetting these parameters prior to each LP call.

Consider the following example to maximize subject to the constraints $X_1 + X_2 \leq 10$ , and $X_1 \geq 0$ , and $X_2 \geq 0$ . The problem is solved by using the following statements:

/* the problem data */
obj = {1 0};
coef = {1 1};
b = {0, 10};

/* embed the objective function in the coefficient matrix */
a = obj // coef;
a = a || {-1, 0};

/* solve the problem */
call lp(rc, x, dual, a, b);
print rc, x, dual;

Figure 23.175: Solution to a Constrained Linear Problem

rc
0

x
10
0
10

dual
-1	1