MEAN Function
MEAN (x <, method> <, param> ) ;
The MEAN function computes a sample mean of data. The arguments are as follows:
- x
-
specifies an
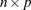numerical matrix. The MEAN function computes means of the 
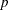columns of this matrix.
- method
-
specifies the method used to compute the mean. This argument is optional. The following are valid values:
- “arithmetic”
-
specifies that arithmetic means be computed. This is the default value.
- “trimmed”
-
specifies that trimmed means be computed. The number of observations that are trimmed is determined by the param option.
- “winsorized”
-
specifies that Winsorized means be computed. The number of observations that are Winsorized is determined by the param option.
- param
-
specifies the number of observations trimmed or Winsorized. (This argument is ignored when “arithmetic” is specified for the method argument.) The default value for param is 0.1, which corresponds to trimming or Winsorizing 10% of the observations with the lowest values and 10% of the observations with the largest values.
The method argument is not case-sensitive. The first four characters are used to determine the value. For example, “WINS”, “Winsor”, and “winsorized” specify the same option.
The MEAN function uses the same algorithms as the UNIVARIATE procedure for computing the means, trimmed means, and Winsorized means. For additional details and formulas, see the UNIVARIATE procedure documentation (especially the TRIMMED= and WINSORIZED= options) in the Base SAS Procedures Guide: Statistical Procedures.
The param argument determines how many observations are trimmed (or Winsorized). The value for this argument can be an integer or a
proportion. If the value is an integer 
, then observations are trimmed, provided that is between 0 and half the number of nonmissing observations. If value is a proportion in the interval 
, then the number of observations trimmed is equal to the smallest integer that is greater than or equal to 
, where 
is the number of nonmissing observations.
The following example demonstrates basic usage:
x = {5,6,6,6,7,7,7,8,8,15};
mean = mean(x);
trim = mean(x, "trimmed", 0.2); /* 20% of obs */
winsor = mean(x, "winsorized", 1); /* one obs */
print mean trim winsor;
Figure 23.189: Arithmetic, Trimmed, and Winsorized Means
| mean | trim | winsor |
|---|---|---|
| 7.5 | 6.8333333 | 6.9 |
The MEAN function operates on columns of matrices. If x is an matrix, the function returns a 
row vector. The value of the 
th element is the mean for the th column of the matrix, as the following example demonstrates:
x = {5 1 10,
6 2 3,
6 8 5,
6 7 9,
7 2 13};
mean = mean(x);
print mean;
Figure 23.190: Arithmetic Mean of Columns
| mean | ||
|---|---|---|
| 6 | 4 | 8 |
Missing values in a column are excluded from the computation. The default behavior of the MEAN function is identical to the
subscript reduction operator that computes the mean. That is, mean(x) and x[:,] both compute the means of the columns of x. See the section Subscript Reduction Operators for more information about subscript reduction operators.