TSMLOCAR Call :: SAS/IML(R) 12.1 User's Guide

TSMLOCAR Call

CALL TSMLOCAR (arcoef, ev, nar, aic, start, finish, data <*>, maxlag <*>, opt <*>, missing <*>, print ) ;

The TSMLOCAR subroutine analyzes nonstationary or locally stationary time series by using the minimum AIC procedure.

The input arguments to the TSMLOCAR subroutine are as follows:

data

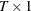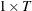specifies a $T \times 1$ (or $1 \times T$ ) data vector.

maxlag

specifies the maximum lag of the AR process. This value should be less than half the length of locally stationary spans. The default is maxlag=10.

opt

specifies an options vector.

opt[1]: specifies the mean deletion option. The mean of the original data is deleted if opt[1]=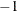. An intercept coefficient is estimated if opt[1]=1. If opt[1]=0, the original input data are processed assuming that the mean value of the input series is 0. The default is opt[1]=0.
opt[2]: specifies the span length to be used when breaking up the time series into separate blocks. By default, , which forces all of the time series values into a single span.
opt[3]: specifies the minimum AIC option. If opt[3]=0, the maximum lag AR process is estimated. If opt[3]=1, the minimum AIC procedure is performed. The default is opt[3]=1.

missing

specifies the missing value option. By default, only the first contiguous observations with no missing values are used (missing=0). The missing=1 option ignores observations with missing values. If you specify the missing=2 option, the missing values are replaced with the sample mean. print] specifies the print option. By default, printed output is suppressed (print=0). The print=1 option prints the AR estimation result, while the print=2 option plots the power spectral density in addition to the AR estimates.

The TSMLOCAR subroutine returns the following values:

arcoef: refers to an 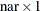$\mbox{nar} \times 1$ AR coefficient vector of the final model if the intercept estimate is not included. If opt[1]=1, the first element of the arcoef vector is an intercept estimate.
ev: refers to the error variance.
nar: is the selected AR order of the final model. If opt[3]=0, nar=maxlag.
aic: refers to the minimum AIC value of the final model.
start: refers to the starting position of the input series, which corresponds to the first observation of the final model.
finish: refers to the ending position of the input series, which corresponds to the last observation of the final model.

The TSMLOCAR subroutine analyzes nonstationary (or locally stationary) time series by using the minimum AIC procedure. The data of length is divided into locally stationary subseries, which consist of $\frac{T}{J}$ observations. See the section Nonstationary Time Series for details.