VAR Function
VAR (x) ;
The VAR function computes a sample variance of data.
The arguments to the VAR function are as follows:
- x
-
specifies an
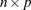 numerical matrix. The VAR function computes the variance of the
numerical matrix. The VAR function computes the variance of the 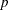 columns of this matrix.
columns of this matrix.
The VAR function computes the sample variance of a column vector x as ![]() where
where ![]() is the number of nonmissing values of x and any missing values have been excluded. When x is a matrix, the sample variance is computed for each column, as the following example shows:
is the number of nonmissing values of x and any missing values have been excluded. When x is a matrix, the sample variance is computed for each column, as the following example shows:
x = {5 1 10,
6 2 3,
6 8 5,
6 7 9,
7 2 13};
var = var(x);
print var;
Figure 23.367: Variance of Columns
| var | ||
|---|---|---|
| 0.5 | 10.5 | 16 |
The following statement computes the standard deviation of each column:
sd = sqrt(var(x));
The VAR function returns a missing value for columns with fewer than two nonmissing observations.