RANDMVT Function
RANDMVT (N, DF, Mean, Cov ) ;
The RANDMVT function returns an ![]() matrix that contains
matrix that contains ![]() random draws from the Student’s
random draws from the Student’s ![]() distribution with DF degrees of freedom, mean vector Mean, and covariance matrix Cov.
distribution with DF degrees of freedom, mean vector Mean, and covariance matrix Cov.
The inputs are as follows:
- N
-
is the number of desired observations sampled from the multivariate Student’s
 distribution.
distribution.
- DF
-
is a scalar value that represents the degrees of freedom for the
 distribution.
distribution.
- Mean
-
is a
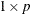 vector of means.
vector of means.
- Cov
-
is a
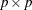 symmetric positive definite variance-covariance matrix.
symmetric positive definite variance-covariance matrix.
If ![]() follows a multivariate
follows a multivariate ![]() distribution with
distribution with ![]() degrees of freedom, mean vector
degrees of freedom, mean vector ![]() , and variance-covariance matrix
, and variance-covariance matrix ![]() , then
, then
-
the probability density function for
 is
is
![\[ f(x; \nu , \mu , \Sigma ) = \frac{\Gamma ((\nu +p)/2)}{|\Sigma |^{1/2} (\pi \nu )^{p/2}\Gamma (\nu /2)} \left( 1+ \frac{(x-\mu ) \Sigma ^{-1} (x-\mu )^ T}{\nu } \right)^{-(\nu +p)/2} \]](images/imlug_modlib0077.png)
-
if
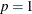 , the probability density function reduces to a univariate Student’s
, the probability density function reduces to a univariate Student’s  distribution.
distribution.
-
the expected value of
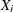 is
is 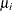 .
.
-
the covariance of
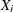 and
and 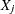 is
is 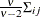 when
when 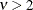 .
.
The following example generates 1,000 samples from a two-dimensional ![]() distribution with 7 degrees of freedom, mean vector
distribution with 7 degrees of freedom, mean vector ![]() , and covariance matrix
, and covariance matrix S. Each row of the returned matrix x is a row vector sampled from the ![]() distribution. The example computes the sample mean and covariance and compares them with the expected values.
distribution. The example computes the sample mean and covariance and compares them with the expected values.
call randseed(1);
N = 1000;
DF = 4;
Mean = {1 2};
S = {1 1, 1 5};
x = RandMVT( N, DF, Mean, S );
SampleMean = x[:,];
y = x - SampleMean;
SampleCov = y`*y / (n-1);
Cov = (DF/(DF-2)) * S;
print SampleMean Mean, SampleCov Cov;
Figure 24.11: Estimated Mean and Covariance Matrix
| SampleMean | Mean | ||
|---|---|---|---|
| 1.0432737 | 2.0316188 | 1 | 2 |
| SampleCov | Cov | ||
|---|---|---|---|
| 2.1564643 | 2.2468668 | 2 | 2 |
| 2.2468668 | 9.6246181 | 2 | 10 |
In the preceding example, the columns (marginals) of x do not follow univariate ![]() distributions. If you want a sample whose marginals are univariate
distributions. If you want a sample whose marginals are univariate ![]() , then you need to scale each column of the output matrix:
, then you need to scale each column of the output matrix:
x = RandMVT( N, DF, Mean, S ); StdX = x / sqrt(T(vecdiag(S))); /* StdX columns are univariate t */
Equivalently, you can generate samples whose marginals are univariate ![]() by passing in a correlation matrix instead of a general covariance matrix.
by passing in a correlation matrix instead of a general covariance matrix.
For further details about sampling from the multivariate ![]() distribution, see Kotz and Nadarajah (2004).
distribution, see Kotz and Nadarajah (2004).