Kuhn-Tucker Conditions
The nonlinear programming (NLP) problem with one objective function ![]() and
and ![]() constraint functions
constraint functions ![]() , which are continuously differentiable, is defined as follows:
, which are continuously differentiable, is defined as follows:
|
|
|
|
|
|
|
|
|
|
|
|
In the preceding notation, ![]() is the dimension of the function
is the dimension of the function ![]() , and
, and ![]() is the number of equality constraints. The linear combination of objective and constraint functions
is the number of equality constraints. The linear combination of objective and constraint functions
|
|
is the Lagrange function, and the coefficients ![]() are the Lagrange multipliers.
are the Lagrange multipliers.
If the functions ![]() and
and ![]() are twice differentiable, the point
are twice differentiable, the point ![]() is an isolated local minimizer of the NLP problem, if there exists a vector
is an isolated local minimizer of the NLP problem, if there exists a vector ![]() that meets the following conditions:
that meets the following conditions:
-
Kuhn-Tucker conditions
![\[ \begin{array}{ll} c_ i(x^*) = 0 , & i = 1, \ldots ,m_ e \\ c_ i(x^*) \ge 0 , ~ ~ \lambda _ i^* \ge 0, ~ ~ \lambda _ i^* c_ i(x^*) = 0 , & i = m_ e+1, \ldots ,m \\ \nabla _ x L(x^*,\lambda ^*) = 0 \end{array} \]](images/imlug_nonlinearoptexpls0077.png)
-
second-order condition
Each nonzero vector
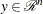 with
with
![\[ y^ T \nabla _ x c_ i(x^*) = 0 i = 1,\ldots ,m_ e ,\; \mbox{ and } \forall i\in {m_ e+1,\ldots ,m}; \lambda _ i^* > 0 \]](images/imlug_nonlinearoptexpls0079.png)
satisfies
![\[ y^ T \nabla _ x^2 L(x^*,\lambda ^*) y > 0 \]](images/imlug_nonlinearoptexpls0080.png)
In practice, you cannot expect the constraint functions ![]() to vanish within machine precision, and determining the set of active constraints at the solution
to vanish within machine precision, and determining the set of active constraints at the solution ![]() might not be simple.
might not be simple.