Language Reference

LCP Call

CALL LCP (rc, w, z, m, q <, epsilon> );

The LCP subroutine solves the linear complementarity problem:

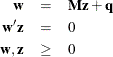
$\begin{eqnarray*} \mb{w} & = & \mb{Mz} + \mb{q} \\ \mb{w}^{\prime } \mb{z} & = & 0 \\ \mb{w},\mb{z} & \geq & 0 \end{eqnarray*}$

That is, given a matrix $\mb{M}$ and a vector $\mb{q}$ , the LCP subroutine computes orthogonal, nonnegative vectors $\mb{w}$ and $\mb{z}$ which satisfy the previous equations.

The input arguments to the LCP subroutine are as follows:

m

is an $m \times m$ matrix.

q

is an 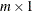$m \times 1$ matrix.

epsilon

is a scalar that defines virtual zero. The default value of epsilon is 1E $-$ 8.

The LCP subroutine returns the following matrices:

rc

returns one of the following scalar return codes:

rc	Termination
0	A solution is found.
1	No solution is possible.
5	The solution is numerically unstable.
6	The subroutine could not obtain enough memory.

w

returns an m-element column vector

z

returns an m-element column vector

The following statements give a simple example:

q = {1, 1};
m = {1 0,
     0 1};
call lcp(rc, w, z, m, q);
print rc, w, z;

Figure 24.189: Solution to a Linear Complementarity Problem

rc
0

w
1
1

z
0
0

The next example shows the relationship between quadratic programming and the linear complementarity problem. Consider the linearly constrained quadratic program:

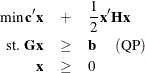
$\begin{eqnarray*} \min \mb{c}^{\prime } \mb{x} & + & \frac{1}{2}\mb{x}^{\prime }\mb{Hx} \\ \mbox{st. } \mb{Gx} & \geq & \mb{b} ~ ~ ~ ~ ~ (\mbox{QP}) \\ \mb{x} & \geq & 0 ~ \end{eqnarray*}$

If $\mb{H}$ is positive semidefinite, then a solution to the Kuhn-Tucker conditions solves QP. The Kuhn-Tucker conditions for QP are

$\begin{eqnarray*} \mb{c} + \mb{Hx} & = & \mu + \mb{G}^{\prime } { \lambda } \\ \lambda ^{\prime } (\mb{Gx}- \mb{b}) & = & 0 \\ {\mu }^{\prime } \mb{x} & = & 0 \\ \mb{Gx} & \geq & \mb{b} \\[0.10in] {x, \mu ,\lambda } & \geq & 0 ~ \end{eqnarray*}$

In the linear complementarity problem, let

$\begin{eqnarray*} \mb{M} & = & \left[ \begin{array}{cc} H & -G^{\prime } \\ G & 0 \\ \end{array} \right] \\ \mb{w}^{\prime } & = & ({\mu }^{\prime }\mb{s}^{\prime }) \\ \mb{z}^{\prime } & = & (\mb{x}^{\prime }{ \lambda }^{\prime }) \\ \mb{q}^{\prime } & = & (\mb{c}^{\prime } - \mb{b}) ~ \end{eqnarray*}$

Then the Kuhn-Tucker conditions are expressed as finding $\mb{w}$ and $\mb{z}$ that satisfy

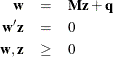
$\begin{eqnarray*} \mb{w} & = & \mb{Mz} + \mb{q} \\ \mb{w}^{\prime }\mb{z} & = & 0 \\ \mb{w},\mb{z} & \geq & 0 ~ \end{eqnarray*}$

From the solution $\mb{w}$ and $\mb{z}$ to this linear complementarity problem, the solution to QP is obtained; namely, $\mb{x}$ is the primal structural variable, $\mb{s}= \mb{Gx}-\mb{b}$ the surpluses, and $\bmu$ and $\blambda$ are the dual variables. Consider a quadratic program with the following data:

$\begin{eqnarray*} \mb{C}^{\prime } & = & (1 2 4 5) ~ ~ ~ ~ ~ \mb{B}^{\prime } = ( 1 1 ) \\[0.10in] \mb{H} & = & \left[ \begin{array}{rrrr} 100 & 10 & 1 & 0 \\ 10 & 100 & 10 & 1 \\ 1 & 10 & 100 & 10 \\ 0 & 1 & 10 & 100 \end{array} \right] \\[0.10in] \mb{G} & = & \left[ \begin{array}{rrrr} 1 & 2 & 3 & 4 \\ 10 & 20 & 30 & 40 \end{array} \right] \\ \end{eqnarray*}$

This problem is solved by using the LCP subroutine as follows:

/*---- Data for the Quadratic Program -----*/
c = {1, 2, 3, 4};
h = {100 10 1 0, 10 100 10 1, 1 10 100 10, 0 1 10 100};
g = {1 2 3 4, 10 20 30 40};
b = {1, 1};

/*----- Express the Kuhn-Tucker Conditions as an LCP ----*/
m = h || -g`;
m = m // (g || j(nrow(g),nrow(g),0));
q = c // -b;

/*----- Solve for a Kuhn-Tucker Point --------*/
call lcp(rc, w, z, m, q);

/*------ Extract the Solution to the Quadratic Program ----*/
x = z[1:nrow(h)];
print rc x;

Figure 24.190: Solution to a Quadratic Programming Problem

rc	x
0	0.0307522
	0.0619692
	0.0929721
	0.1415983