Language Reference
CALL MILPSOLVE (rc, objvalue, x, relgap, c, a, b <*>, cntl <*>, coltype <*>, rowsense <*>, range <*>, l <*>, u );
The MILPSOLVE subroutine solves a mixed integer linear programming problem. For complete functionality the SAS/OR product must also be installed, otherwise the maximum number of variables and maximum number of constraints is restricted to 500.
The input arguments to the MILPSOLVE subroutine are as follows:
- c
-
is a vector of dimension n of objective function coefficients. A missing value is treated as 0.
- a
-
is an
 matrix of the technological coefficients. A missing value is treated as 0.
matrix of the technological coefficients. A missing value is treated as 0.
- b
-
is a vector of dimension m of constraints’ right-hand sides (RHS). For a range constraint, b is the constraint upper bound. A missing value is treated as 0.
- cntl
-
is an optional vector that contains the control parameters for the MILPSOLVE subroutine. The vector can contain from one to 14 options. These options are a subset of the options that are supported by the OPTMILP procedure in SAS/OR software. For a detailed description of the options, see SAS/OR User's Guide: Mathematical Programming. A default value is used when an option is not specified or its value is a missing value. If cntl=(objsense, printlevel, maxtime, maxnodes, relobjgap, presolver, cuts, heuristics, probe, nodesel, varsel, conflictsearch, inttol, tol), then
- objsense
-
specifies whether the problem is a minimization or a maximization problem, where 1 specifies a minimization problem and
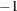 specifies a maximization problem. The default value is 1.
specifies a maximization problem. The default value is 1.
- printlevel
-
specifies the type of messages printed to the log. A value of 0 prints warning and error messages only, whereas 1 prints solution information in addition to warning and error messages. The default value is 0.
- maxtime
-
specifies an upper bound of running time in seconds. The default value is effectively unbounded.
- maxnodes
-
specifies the maximum number of branch-and-bound nodes to be processed. The default value is no limit.
- relobjgap
-
specifies a stopping criterion that is based on the best integer objective and the objective of the best remaining node. The stopping criterion is
![\[ |\mbox{BestInteger} - \mbox{BestBound}| / (10^{-10} + |\mbox{BestBound}|) \]](images/imlug_langref0780.png)
The default value is
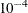 .
.
- presolver
-
specifies a presolve option, where 0 specifies that no presolve is performed, and 1 specifies that an automatic presolve is performed. The default value is 1.
- cuts
-
specifies a cuts option, where 0 specifies that no cuts are made, and 1 specifies that automatic cuts are made. The default value is 0.
- heuristics
-
specifies a heuristics option, where 0 specifies that no heuristics are used, and 1 specifies that heuristics are automatically used. The default value is 1.
- probe
-
specifies a probe option, where 0 specifies that no probing is performed, and 1 specifies that probing is automatically performed. The default value is 1.
- nodesel
-
specifies the node selection strategy, where
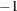 specifies automatic selection, 0 chooses the node that has the best relaxed objective, 1 chooses the node that has the best
estimate of the integer objective value, and 2 chooses the most recently created node. The default value is
specifies automatic selection, 0 chooses the node that has the best relaxed objective, 1 chooses the node that has the best
estimate of the integer objective value, and 2 chooses the most recently created node. The default value is 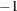 .
.
- varsel
-
specifies the rule for selecting the branching variable, where
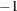 uses automatic branching variable selection, 0 chooses the variable that has maximum infeasibility, 1 chooses the variable
that has minimum infeasibility, 2 chooses a branching variable based on pseudocost, and 3 uses the strong branching variable
selection strategy. The default value is
uses automatic branching variable selection, 0 chooses the variable that has maximum infeasibility, 1 chooses the variable
that has minimum infeasibility, 2 chooses a branching variable based on pseudocost, and 3 uses the strong branching variable
selection strategy. The default value is 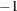 .
.
- conflictsearch
-
specifies a conflict search option, where 0 specifies no conflict search and 1 specifies automatic conflict search. The default value is 1.
- inttol
-
specifies the amount by which an integer variable value can differ from an integer and still be considered integer feasible. . The value can be any number between 0.0 and 0.5. The default value is
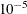 .
.
- tol
-
specifies a feasibility and optimality tolerance. The value can be any number between
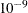 and
and 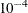 . The default value is
. The default value is 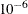 .
.
- coltype
-
is an optional column vector of dimension n that specifies the type of each variable. The values can be C, B, or I for continuous, binary, or integer variable. If this vector is missing or coltype[j] has a missing value, the solver treats variable j as a binary variable if both l and u bounds are not specified or as a continuous variable otherwise.
- rowsense
-
is an optional row vector of dimension m that specifies the sense of each constraint. The values can be E, L, G, or R for equal, less than or equal to, greater than or equal to, or range constraint. If this vector is missing, the solver treats the constraints as E type constraints.
- range
-
is an optional row vector of dimension m that specifies the range of the constraints. The row sense of a range constraint is R. For the non-range constraints, the corresponding values are ignored. For a range constraint, the range value is the difference between its constraint lower bound and its constraint upper bound b, so it must be nonnegative.
- l
-
is an optional column vector of dimension n that specifies lower bounds on the decision variables. If you do not specify l or l[j] has a missing value, then the lower bound of variable j is assumed to be 0.
- u
-
is an optional column vector of dimension n that specifies upper bounds on the decision variables. If you do not specify u or u[j] has a missing value, the upper bound of variable j is assumed to be 1 for a binary or integer variable, or infinity for the continuous variable.
The MILPSOLVE subroutine returns the following values:
- rc
-
returns one of the following scalar return codes:
rc
Termination Reason
0
The solution is integer optimal.
1
The time limit was exceeded.
2
The number of node limit was exceeded.
3
The solution is infeasible.
4
The solution is unbounded or infeasible.
5
The subroutine could not obtain enough memory.
6
The subroutine failed to solve the problem.
- objvalue
-
returns the optimal or final objective value at termination.
- x
-
returns the current primal solution in a column vector of length n.
- relgap
-
returns the relative gap between the current best integer objective and the objective of the best remaining node.
The MILPSOLVE subroutine is a solver for general mixed integer linear programs (MILPs).
A standard mixed integer linear program has the formulation:
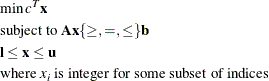
If only c, ![]() , and
, and ![]() are present, then the MILPSOLVE subroutine solves the following integer programming problem by default:
are present, then the MILPSOLVE subroutine solves the following integer programming problem by default:
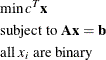
The MILPSOLVE subroutine implements a linear-programming-based branch-and-bound algorithm. This divide-and-conquer approach attempts to solve the original problem by solving linear programming relaxations of a sequence of smaller subproblems. The MILPSOLVE subroutine also implements advanced techniques such as presolving, probing, generating cutting planes, and applying primal heuristics to improve the efficiency of the overall algorithm. These techniques are explained in more detail in the chapter "The OPTMILP Procedure" in SAS/OR User's Guide: Mathematical Programming.
Consider the following example:
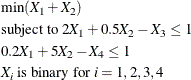
The problem is solved by using the following statements:
object = { 1 1 0 0 };
coef = { 2 .5 -1 0,
.2 5 0 -1};
b = { 1, 1 };
rowsense = {L,L};
cntl = -1;
call milpsolve(rc,objv,x,relgap,object,coef,b,cntl,,rowsense);
print objv, x, relgap;