Language Reference

NDX2SUB Function

NDX2SUB (dim, indices );

The NDX2SUB function is part of the IMLMLIB library . The NDX2SUB function converts indices of a matrix into subscripts for the matrix. The arguments are as follows:

dim

specifies the dimensions of the matrix. For example, the value of this argument might be the 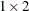$1\times 2$ vector that is returned from the DIMENSION function .

indices

specifies the elements of a matrix, enumerated in row-major order.

The indices of an $n\times p$ matrix are the elements $1, 2, \ldots , np$. The indices enumerate the elements in row-major order: the first p indices enumerate the first row, the next p indices enumerate the second row, and so forth. The NDX2SUB function converts indices to subscripts, which are pairs $(i,j)$ such that $1\leq i \leq n$ and $1\leq j \leq p$.

You can use the module to display the rows and columns of elements that satisfy a certain condition. For example, the following statements locate all the even numbers in a matrix and then call the NDX2SUB function to find the subscripts of the even elements: 

x = {1  2  3,
     4  5  6,
     7  8  9,
    10 11 12};
idx = loc( mod(x, 2)=0 );
dim = nrow(x) || ncol(x);
s = ndx2sub(dim, idx);
print s;

Figure 24.229: Subscripts That Correspond to Indices

s
1 2
2 1
2 3
3 2
4 1
4 3 




            

            


            
You can also use the NDX2SUB function to keep track of indices and subscripts of multidimensional arrays. Although the SAS/IML
               language does not support multidimensional arrays, a common technique is to store the elements of a $d_1 \times d_2 \times \ldots \times d_ k$ array in a two-dimensional matrix with $d_1 \times d_2 \times \ldots \times d_{k-1}$ rows and $d_ k$ columns. For example, you can store the contents of four $3\times 3$ arrays in a single $12\times 3$ matrix, as shown in the following program: 
            


/* Store four 3x3 matrices in a 12x3 matrix
  (each group of three rows is a matrix) */
dim = {4 3 3};
m = j(12, 3);
p = 9; /* = prod(dim[2:ncol(dim)]) */
do i = 1 to 4;
   startNdx = 1 + (i-1)*p;
   endNdx   = i*p;
   ndx = startNdx:endNdx; /* get indices for i_th matrix */
   m[ndx] = i; /* assign or extract matrix */
   subscripts = ndx2sub(dim, ndx); /* or get subscripts */
end;
print m;



   

            


Figure 24.230: Storing Smaller Matrices inside a Larger Matrix

               

                  

                     
                     

                        
                        
                        

                           
                           

                              
                              








m
                                       
                                    




1
                                       
                                       1
                                       
                                       1
                                       
                                    



1
                                       
                                       1
                                       
                                       1
                                       
                                    



1
                                       
                                       1
                                       
                                       1
                                       
                                    



2
                                       
                                       2
                                       
                                       2
                                       
                                    



2
                                       
                                       2
                                       
                                       2
                                       
                                    



2
                                       
                                       2
                                       
                                       2
                                       
                                    



3
                                       
                                       3
                                       
                                       3
                                       
                                    



3
                                       
                                       3
                                       
                                       3
                                       
                                    



3
                                       
                                       3
                                       
                                       3
                                       
                                    



4
                                       
                                       4
                                       
                                       4
                                       
                                    



4
                                       
                                       4
                                       
                                       4
                                       
                                    



4
                                       
                                       4
                                       
                                       4