Language Reference

NORM Function

Subsections:

Methods for Vector Norms
Methods for Matrix Norms

NORM (x, <, method> );

The NORM function computes the vector or matrix norm of x. The norm depends on the metric specified by the method argument. The arguments are as follows:

x: specifies a numeric vector with n elements or an 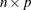$n\times p$ numeric matrix.
method: is an optional argument that specifies the method used to specify the norm. The method argument is either a numeric value, method 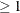$\geq 1$ , or a case-insensitive character value. The valid options are given in the following sections.

Methods for Vector Norms

If x is a vector, then a vector norm is computed. The following are valid values of the method argument:

"L1"

specifies that the function compute the 1-norm: 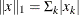$\| x \| _1 = \Sigma _ k |x_ k |$ . An equivalent alias is "CityBlock" or "Manhattan".

"L2"

specifies that the function compute the Euclidean 2-norm: 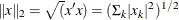$\| x \| _2 = \sqrt (x^\prime x) = (\Sigma _ k |x_ k |^2 )^{1/2}$ . This is the default value. An equivalent alias is "Euclidean" or "Frobenius".

"LInf"

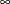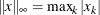specifies that the function compute the $\infty$ -norm: $\| x \| _\infty = \max _ k |x_ k |$ .

An equivalent alias is "Chebyshev".

p

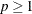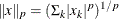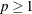is a numeric value, $p \geq 1$ , that specifies the p-norm: $\| x \| _ p = (\Sigma _ k |x_ k |^ p )^{1/p}$ , $p\geq 1$ .

Methods for Matrix Norms

For an $n\times p$ matrix A such that $n>1$ and $p>1$ , the method argument has the following valid values:

"Frobenius": specifies the Frobenius norm: 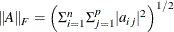$\| A \| _ F = \left( \Sigma _{i=1}^ n \Sigma _{j=1}^ p |a_{ij} |^2 \right)^{1/2}$ . This is the default value.
"L1": specifies the matrix 1-norm: 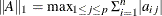$\| A \| _1 = \max _{1\leq j\leq p}\Sigma _{i=1}^ n |a_{ij} |$ . This norm computes the maximum of the absolute column sums.
"L2": specifies the matrix 2-norm, which is equivalent to the square root of the largest eigenvalue of the 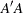$A^\prime A$ matrix. This quantity can be expensive to compute because the function internally computes eigenvalues.
"LInf": specifies the 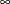$\infty$ -norm: $\| A \| _\infty = \max _{1\leq i\leq n}\Sigma _{j=1}^ p |a_{ij} |$ . This norm computes the maximum of the absolute row sums.

The matrix p-norm is not available unless $p \in \{ 1,2, \infty \}$ .

The following statements compute vector norms:

/* compute vector norms */
v = 1:5;
vn1 = norm(v, "L1");
vn2 = norm(v, "L2");
vnInf = norm(v, "LInf");
print vn1 vn2 vnInf;

Figure 24.243: Vector Norms

vn1	vn2	vnInf
15	7.4161985	5

You can also compute matrix norms, as follows:

x = {1 2, 3 4};
mn1 = norm(x, "L1");
mnF = norm(x, "Frobenius");
mnInf = norm(x, "LInf");
print mn1 mnF mnInf;

Figure 24.244: Matrix Norms

mn1	mnF	mnInf
6	5.4772256	7

The NORM function returns a missing value if any element of the argument contains a missing value.