Language Reference

RATES Function

RATES (rates, oldfreq, newfreq);

The RATES function computes a column vector of (per-period, such as per-year) interest rates converted from one base to another. The arguments to the RATES function are as follows:

rates: is an 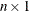$n \times 1$ column vector of rates that correspond to the old base. Elements should be positive.
oldfreq: is a scalar that represents the old base. If positive, it represents discrete compounding as the reciprocal of the number of compoundings per period. If zero, it represents continuous compounding. If –1, the rates represent discount factors. No other negative values are accepted.
newfreq: is a scalar that represents the new base. If positive, it represents discrete compounding as the reciprocal of the number of compoundings per period. If zero, it represents continuous compounding. If –1, the rates represent discount factors. No other negative values are accepted.

Let $D(t)$ be the discount function, which is the present value of a unit amount to be received t periods from now. The discount function can be expressed in the following ways:

with per-unit-time-period discount factors $d_ t$ :

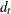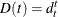
$\begin{equation*} D(t) = d_ t^ t \end{equation*}$
with continuous compounding:

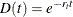
$\begin{equation*} D(t) = e^{-r_ t t} \end{equation*}$
with discrete compounding:

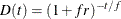
$\begin{equation*} D(t) = (1+fr)^{-t/f} \end{equation*}$

where 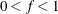$0 < f < 1$ is the frequency, the reciprocal of the number of compoundings per unit time period. The RATES function converts between these three representations.

For example, the following example produces the output shown in Figure 24.318:

rates = T(do(0.1, 0.3, 0.1));
oldfreq = 0;
newfreq = 0;
rates = rates(rates, oldfreq, newfreq);
print rates;

Figure 24.318: Interest Rates

rates
0.1
0.2
0.3