Language Reference

TSPEARS Call

CALL TSPEARS (arcoef, ev, nar, aic, data <*>, maxlag <*>, opt <*>, missing <*>, print );

The TSPEARS subroutine analyzes periodic AR models with the minimum AIC procedure.

The input arguments to the TSPEARS subroutine are as follows:

data

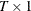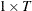specifies a $T \times 1$ (or $1 \times T$) data matrix.

maxlag

specifies the maximum lag of the periodic AR process. This value should be less than 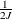$\frac{1}{2J}$ of the input series. The default is maxlag=10.

opt

specifies an options vector.

opt[1]

specifies the mean deletion option. The mean of the original data is deleted if opt[1]=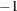$-1$. An intercept coefficient is estimated if opt[1]=1. If opt[1]=0, the original input data are processed assuming that the mean values of input series are zeros. The default is opt[1]=0.

opt[2]

specifies the number of instants per period. By default, opt[2]=1.

opt[3]

specifies the minimum AIC option. If opt[3]=0, the maximum lag AR process is estimated. If opt[3]=1, the minimum AIC procedure is used. The default is opt[3]=1.

missing

specifies the missing value option. By default, only the first contiguous observations with no missing values are used (missing=0). The missing=1 option ignores observations with missing values. If you specify the missing=2 option, the missing values are replaced with the sample mean.

print

specifies the print option. By default, printed output is suppressed (print=0). The print=1 option prints the periodic AR estimates and intermediate process.

The TSPEARS subroutine returns the following values:

arcoef

refers to a periodic AR coefficient matrix of the periodic AR model. If opt[1]=1, the first column of the arcoef matrix is an intercept estimate vector.

ev

refers to the error variance.

nar

refers to the selected AR order vector of the periodic AR model.

aic

refers to the minimum AIC values of the periodic AR model.

The TSPEARS subroutine analyzes the periodic AR model by using the minimum AIC procedure. The data of length T are divided into d periods. There are J instants in one period. See the section Multivariate Time Series Analysis for details.