Nonlinear Optimization Examples

Unconstrained Rosenbrock Function

The Rosenbrock function is defined as

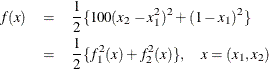
$\begin{eqnarray*} f(x) & = & \frac{1}{2} \{ 100 (x_2 - x_1^2)^2 + (1 - x_1)^2 \} \\ & = & \frac{1}{2} \{ f_1^2(x) + f_2^2(x) \} , \quad x = (x_1,x_2) \end{eqnarray*}$

The minimum function value $f^* = f(x^*) = 0$ is at the point $x^* = (1,1)$ .

The following code calls the NLPTR subroutine to solve the optimization problem:

The NLPTR is a trust-region optimization method. The F_ROSEN module represents the Rosenbrock function, and the G_ROSEN module represents its gradient. Specifying the gradient can reduce the number of function calls by the optimization subroutine. The optimization begins at the initial point $x=(-1.2, 1)$ . For more information about the NLPTR subroutine and its arguments, see the section NLPTR Call. For details about the options vector, which is given by the OPTN vector in the preceding code, see the section Options Vector.

A portion of the output produced by the NLPTR subroutine is shown in Figure 14.1.

Figure 14.1: NLPTR Solution to the Rosenbrock Problem

Optimization Start
Parameter Estimates
N	Parameter	Estimate	Gradient Objective Function
1	X1	-1.200000	-107.800000
2	X2	1.000000	-44.000000

Value of Objective Function = 12.1

Trust Region Optimization

Without Parameter Scaling

CRP Jacobian Computed by Finite Differences

Parameter Estimates	2

Optimization Start
Active Constraints	0	Objective Function	12.1
Max Abs Gradient Element	107.8	Radius	1

Iteration	Function Calls	Objective Function	Objective Function Change	Max Abs Gradient Element	Lambda	Trust Region Radius
1	2	2.36594	9.7341	2.3189	0	1.000
2	5	2.05926	0.3067	5.2875	0.385	1.526
3	8	1.74390	0.3154	5.9934	0	1.086
4	9	1.43279	0.3111	6.5134	0.918	0.372
5	10	1.13242	0.3004	4.9245	0	0.373
6	11	0.86905	0.2634	2.9302	0	0.291
7	12	0.66711	0.2019	3.6584	0	0.205
8	13	0.47959	0.1875	1.7354	0	0.208
9	14	0.36337	0.1162	1.7589	2.916	0.132
10	15	0.26903	0.0943	3.4089	0	0.270
11	16	0.16280	0.1062	0.6902	0	0.201
12	19	0.11590	0.0469	1.1456	0	0.316
13	20	0.07616	0.0397	0.8462	0.931	0.134
14	21	0.04873	0.0274	2.8063	0	0.276
15	22	0.01862	0.0301	0.2290	0	0.232
16	25	0.01005	0.00858	0.4553	0	0.256
17	26	0.00414	0.00590	0.4297	0.247	0.104
18	27	0.00100	0.00314	0.4323	0.0453	0.104
19	28	0.0000961	0.000906	0.1134	0	0.104
20	29	1.67873E-6	0.000094	0.0224	0	0.0569
21	30	6.9582E-10	1.678E-6	0.000336	0	0.0248
22	31	1.3128E-16	6.96E-10	1.977E-7	0	0.00314

Optimization Results
Iterations	22	Function Calls	32
Hessian Calls	23	Active Constraints	0
Objective Function	1.312814E-16	Max Abs Gradient Element	1.9773384E-7
Lambda	0	Actual Over Pred Change	0
Radius	0.003140192

ABSGCONV convergence criterion satisfied.

Optimization Results
Parameter Estimates
N	Parameter	Estimate	Gradient Objective Function
1	X1	1.000000	0.000000198
2	X2	1.000000	-0.000000105

Value of Objective Function = 1.312814E-16

Since $f(x) = \frac{1}{2} \{ f_1^2(x) + f_2^2(x)\}$ , you can also use least squares techniques in this situation. The following code calls the NLPLM subroutine to solve the problem. The output is shown in Figure 14.2.

Figure 14.2: NLPLM Solution Using the Least Squares Technique

Optimization Start
Parameter Estimates
N	Parameter	Estimate	Gradient Objective Function
1	X1	-1.200000	-107.799999
2	X2	1.000000	-44.000000

Value of Objective Function = 12.1

Levenberg-Marquardt Optimization

Scaling Update of More (1978)

Gradient Computed by Finite Differences

CRP Jacobian Computed by Finite Differences

Parameter Estimates	2
Functions (Observations)	2

Optimization Start
Active Constraints	0	Objective Function	12.1
Max Abs Gradient Element	107.7999987	Radius	2626.5613171

Iteration	Function Calls	Objective Function	Objective Function Change	Max Abs Gradient Element	Lambda	Ratio Between Actual and Predicted Change
1	4	2.18185	9.9181	17.4704	0.00804	0.964
2	6	1.59370	0.5881	3.7015	0.0190	0.988
3	7	1.32848	0.2652	7.0843	0.00830	0.678
4	8	1.03891	0.2896	6.3092	0.00753	0.593
5	9	0.78943	0.2495	7.2617	0.00634	0.486
6	10	0.58838	0.2011	7.8837	0.00462	0.393
7	11	0.34224	0.2461	6.6815	0.00307	0.524
8	12	0.19630	0.1459	8.3857	0.00147	0.469
9	13	0.11626	0.0800	9.3086	0.00016	0.409
10	14	0.0000396	0.1162	0.1781	0	1.000
11	15	2.4652E-30	0.000040	4.44E-14	0	1.000

Optimization Results
Iterations	11	Function Calls	16
Jacobian Calls	12	Active Constraints	0
Objective Function	2.46519E-30	Max Abs Gradient Element	4.440892E-14
Lambda	0	Actual Over Pred Change	1
Radius	0.0178062912

ABSGCONV convergence criterion satisfied.

Optimization Results
Parameter Estimates
N	Parameter	Estimate	Gradient Objective Function
1	X1	1.000000	-4.44089E-14
2	X2	1.000000	2.220446E-14

Value of Objective Function = 2.46519E-30

The Levenberg-Marquardt least squares method, which is the method used by the NLPLM subroutine, is a modification of the trust-region method for nonlinear least squares problems. The F_ROSEN module represents the Rosenbrock function. Note that for least squares problems, the m functions $f_1(x),\ldots , f_ m(x)$ are specified as elements of a vector; this is different from the manner in which $f(x)$ is specified for the other optimization techniques. No derivatives are specified in the preceding code, so the NLPLM subroutine computes finite-difference approximations. For more information about the NLPLM subroutine, see the section NLPLM Call.