Sparse Matrix Algorithms

Input Data Description

The ITSOLVER call has the following syntax and arguments: 

   call ITSOLVER (x, error, iter, method, A, b,
                  precond, tol, maxiter, start, history);

The conjugate gradient and minimum residual algorithms (method = ’CG’ or method = ’MINRES’) require A to be symmetric; hence you must specify only the lower triangular part of A, while the remaining algorithms require all nonzero coefficients to be listed. The following table lists valid values for the precond parameter for each class of algorithm.

Table 22.1: Subroutine Definitions and Valid Preconditioners

Method Value

Algorithm

Preconditioners

"CG"

conjugate gradient

"NONE" "IC" "DIAG"

"MINRES"

minimum residual

"NONE" "IC" "DIAG"

"BICG"

biconjugate gradient

"NONE" "MILU"

"CGS"

conjugate gradient squared

"NONE"


x

solution vector

error

final solution error (optional)

iter

resultant number of iterations (optional)

A

three-column matrix of triplets, where the first column contains the value, the next column contains the row indices, and the third column contains the column indices of the nonzero matrix coefficients. The order in which triplets are listed is insignificant. For symmetric matrices specify only the lower triangular part, including the main diagonal (row indices must be greater than or equal to the corresponding column indices). Zero coefficients should not be included. No missing values or duplicate entries are allowed.

b

the right-hand-side vector

precond

preconditioner, default value "NONE"

tol

desired tolerance, default value $10^{-7}$

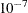
maxiter

maximum number of iterations, default value $10^5$

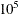
start

initial guess

history

the history of errors for each iteration