LAG Function
Returns values from a queue.
| Category: | Special |
Details
The Basics
If the LAG function
returns a value to a character variable that has not yet been assigned
a length, by default the variable is assigned a length of 200.
The LAG functions, LAG1,
LAG2, ..., LAGn return values
from a queue. LAG1 can also be written as LAG. A LAGn function stores a value in a queue and returns
a value stored previously in that queue. Each occurrence of a LAGn function in a program generates its own queue
of values.
The queue for each occurrence
of LAGn is initialized with n missing values, where n is the length of the queue (for example, a LAG2 queue is initialized
with two missing values). When an occurrence of LAGn is executed, the value at the top of its queue
is removed and returned, the remaining values are shifted upwards,
and the new value of the argument is placed at the bottom of the queue.
Hence, missing values are returned for the first n executions of each occurrence of LAGn, after which the lagged values of the argument
begin to appear.
Memory Limit for the LAG Function
When the LAG function
is compiled, SAS allocates memory in a queue to hold the values of
the variable that is listed in the LAG function. For example, if the
variable in function LAG100(x) is numeric with a length of 8 bytes,
then the memory that is needed is 8 times 100, or 800 bytes. Therefore,
the memory limit for the LAG function is based on the memory that
SAS allocates, which varies with different operating environments.
Examples
Example 1: Generating Two Lagged Values
Example 2: Generating Multiple Lagged Values in BY-Groups
/***************************************************************************/
/* This program generates up to three lagged values. By increasing the */
/* size of the array and the number of assignment statements that use */
/* the LAGn functions, you can generate as many lagged values as needed. */
/***************************************************************************/
/* Create starting data. */
data old;
input start end;
datalines;
1 1
1 2
1 3
1 4
1 5
1 6
1 7
2 1
2 2
3 1
3 2
3 3
3 4
3 5
;
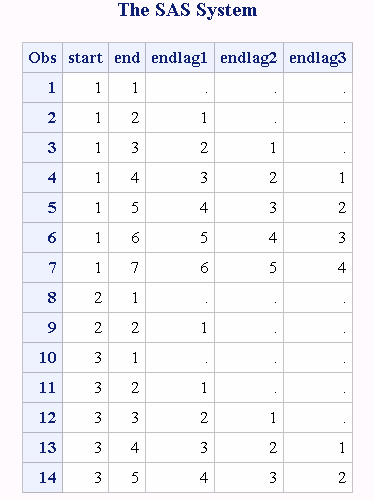
data new(drop=i count);
set old;
by start;
/* Create and assign values to three new variables. Use ENDLAG1- */
/* ENDLAG3 to store lagged values of END, from the most recent to the */
/* third preceding value. */
array x(*) endlag1-endlag3;
endlag1=lag1(end);
endlag2=lag2(end);
endlag3=lag3(end);
/* Reset COUNT at the start of each new BY-Group */
if first.start then count=1;
/* On each iteration, set to missing array elements */
/* that have not yet received a lagged value for the */
/* current BY-Group. Increase count by 1. */
do i=count to dim(x);
x(i)=.;
end;
count + 1;
run;
proc print;
run;
Example 3: Computing the Moving Average of a Variable
/* Title: Compute the moving average of a variable
Goal: Compute the moving average of a variable through the entire data set,
of the last n observations and of the last n observations within a
BY-group.
Input:
*/
data x;
do x=1 to 10;
output;
end;
run;
/* Compute the moving average of the entire data set. */
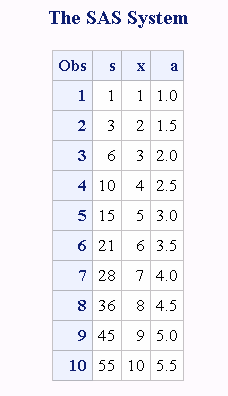
data avg;
retain s 0;
set x;
s=s+x;
a=s/_n_;
run;
proc print;
run;
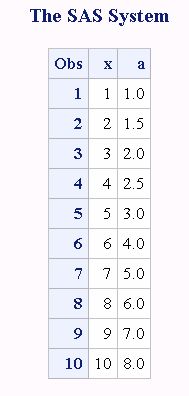
/* Compute the moving average of the last 5 observations. */
%let n = 5;
data avg (drop=s);
retain s;
set x;
s = sum (s, x, -lag&n(x)) ;
a = s / min(_n_, &n);
run;
proc print;
run;
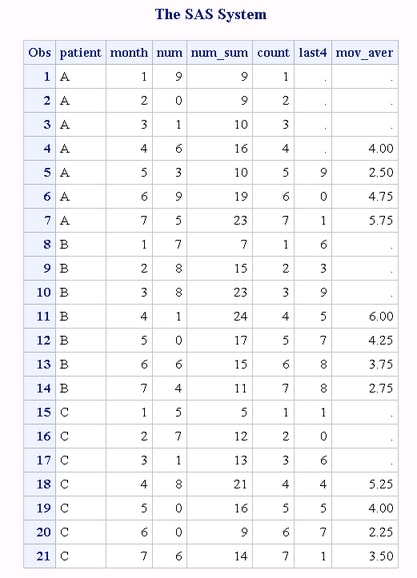
/* Compute the moving average within a BY-group of last n observations.
For the first n-1 observations within the BY-group, the moving average
is set to missing. */
data ds1;
do patient='A','B','C';
do month=1 to 7;
num=int(ranuni(0)*10);
output;
end;
end;
run;
proc sort;
by patient;
%let n = 4;
data ds2;
set ds1;
by patient;
retain num_sum 0;
if first.patient then do;
count=0;
num_sum=0;
end;
count+1;
last&n=lag&n(num);
if count gt &n then num_sum=sum(num_sum,num,-last&n);
else num_sum=sum(num_sum,num);
if count ge &n then mov_aver=num_sum/&n;
else mov_aver=.;
run;
proc print;
run;Example 4: Generating a Fibonacci Sequence of Numbers
The following example
generates a Fibonacci sequence of numbers. You start with 0 and 1,
and then add the two previous Fibonacci numbers to generate the next
Fibonacci number.
Example 5: Using Expressions for the LAG Function Argument
The following program
uses an expression for the value of argument and creates a data set that contains the values for X, Y, and Z.
LAG dequeues the previous values of the expression and enqueues the
current value.
Copyright © SAS Institute Inc. All rights reserved.