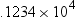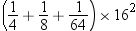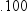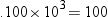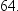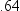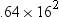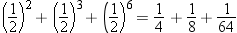Numeric Precision in SAS Software
How SAS Stores Numeric Values
To store numbers of large magnitude and to perform
computations that require many digits of precision to the right of
the decimal point, SAS stores all numeric values using floating-point,
or real binary, representation. Floating-point representation is an
implementation of what is generally known as scientific notation,
in which values are represented as numbers between 0 and 1 times a
power of 10. The following is an example of a number in scientific
notation:
Floating-point representation
is a form of scientific notation, except that on most CPUs the base
is not 10, but is either 2 or 16. The following table summarizes various
representations of floating-point numbers that are stored in 8 bytes.
SAS uses truncated floating-point
numbers via the LENGTH statement, which reduces the number of mantissa
bits. For more information about the effects of truncated lengths,
see Storing Numbers with Less Precision.
Troubleshooting Problems Regarding Floating-Point Representation
Overview
In most situations,
the way that SAS stores numeric values does not affect you as a user.
However, floating-point representation can account for anomalies
that you might notice in SAS program behavior. The following sections
identify the types of problems that can occur in various operating
environments and how you can anticipate and avoid them.
Floating-Point Representation on IBM Mainframes
SAS for z/OS
uses the traditional IBM mainframe floating-point representation as
follows:
SEEEEEEE MMMMMMMM MMMMMMMM MMMMMMMM byte 1 byte 2 byte 3 byte 4 MMMMMMMM MMMMMMMM MMMMMMMM MMMMMMMM byte 5 byte 6 byte 7 byte 8
This representation
corresponds to bytes of data with each character being 1 bit, as follows:
The exponent has a base associated with it. Do not
confuse this with the base in which the exponent is represented; the
exponent is always represented in binary, but the exponent is used
to determine how many times the base should be multiplied by the mantissa.
In the case of the IBM mainframes, the exponent's base is 16. For
other computers, it is commonly either 2 or 16.
-
The seven E characters in byte 1 represent a binary integer known as the characteristic. The characteristic represents a signed exponent and is obtained by adding the bias to the actual exponent. The bias is an offset used to enable both negative and positive exponents with the bias representing 0. If a bias is not used, an additional sign bit for the exponent must be allocated. For example, if a system uses a bias of 64, a characteristic with the value 66 represents an exponent of +2, while a characteristic of 61 represents an exponent of –3.
-
The remaining M characters in bytes 2 through 8 represent the bits of the mantissa. There is an implied radix point before the left-most bit of the mantissa. Therefore, the mantissa is always less than 1. The term radix point is used instead of decimal point because decimal point implies that you are working with decimal (base 10) numbers, which might not be the case. The radix point can be thought of as the generic form of decimal point.
Each bit in the mantissa
represents a fraction whose numerator is 1 and whose denominator is
a power of 2. For example, the leftmost bit in byte 2 represents
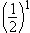 , the next bit represents
, the next bit represents 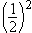 , and so on. In other words, the mantissa is the
sum of a series of fractions such as
, and so on. In other words, the mantissa is the
sum of a series of fractions such as 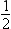 ,
, 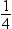 ,
, 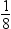 , and so on. Therefore, for any floating-point number
to be represented exactly, you must be able to express it as the previously
mentioned sum. For example, 100 is represented as the following expression:
, and so on. Therefore, for any floating-point number
to be represented exactly, you must be able to express it as the previously
mentioned sum. For example, 100 is represented as the following expression:
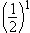 , the next bit represents
, the next bit represents 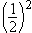 , and so on. In other words, the mantissa is the
sum of a series of fractions such as
, and so on. In other words, the mantissa is the
sum of a series of fractions such as 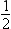 ,
, 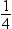 ,
, 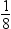 , and so on. Therefore, for any floating-point number
to be represented exactly, you must be able to express it as the previously
mentioned sum. For example, 100 is represented as the following expression:
, and so on. Therefore, for any floating-point number
to be represented exactly, you must be able to express it as the previously
mentioned sum. For example, 100 is represented as the following expression:
To illustrate how the
above expression is obtained, two examples follow. The first example
is in base 10. The value 100 is represented as follows:
100.
Floating-Point Representation on OpenVMS
On OpenVMS, SAS stores numeric
values in the D-floating format, which has the following scheme:
MMMMMMMM MMMMMMMM MMMMMMMM MMMMMMMM byte 8 byte 7 byte 6 byte 5 MMMMMMMM MMMMMMMM SEEEEEEE EMMMMMMM byte 4 byte 3 byte 2 byte 1
In D-floating format,
the exponent is 8 bits instead of 7, but uses base 2 instead of base
16 and a bias of 128, which means the magnitude of the D-floating
format is not as great as the magnitude of the IBM representation.
The mantissa of the D-floating format is, physically, 55 bits. However,
all floating-point values under OpenVMS are normalized, which means
it is guaranteed that the high-order bit is always 1. Because of this
guarantee, there is no need to physically represent the high-order
bit in the mantissa. Therefore, the high-order bit is hidden.
Floating-Point Representation Using the IEEE Standard
The Institute
of Electrical and Electronic Engineers (IEEE) representation is used
by many operating systems, including Windows and UNIX. The IEEE representation
uses an 11-bit exponent with a base of 2 and bias of 1023, which means
that it has much greater magnitude than the IBM mainframe representation,
but sometimes at the expense of 3 bits less in the mantissa. The
value of 1 represented by the IEEE standard is as follows:
3F F0 00 00 00 00 00 00
Precision versus Magnitude
As discussed in previous
sections, floating-point representation enables numbers of very large
magnitude (numbers such as 2 to the 30th power) and high degrees of
precision (many digits to the right of the decimal place). However,
operating systems differ on how much precision and how much magnitude
they use.
In How SAS Stores Numeric Values, you can see that the number of exponent bits and mantissa
bits varies. The more bits that are reserved for the mantissa, the
more precise the number; the more bits that are reserved for the exponent,
the greater the magnitude that the number can have.
Whether precision or
magnitude is more important depends on the characteristics of your
data. For example, if you are working with physics applications,
very large numbers might be needed, and magnitude is probably more
important. However, if you are working with banking applications,
where every digit is important but the number of digits is not great,
then precision is more important. Most often, SAS applications need
a moderate amount of both precision and magnitude, which is sufficiently
provided by floating-point representation.
Computational Considerations of Fractions
Regardless of how much precision is available, there is still the
problem that some numbers cannot be represented exactly. In the decimal
number system, the fraction 1/3 cannot be represented exactly in decimal
notation. Likewise, most decimal fractions (for example, .1) cannot
be represented exactly in base 2 or base 16 numbering systems. This
is the principal reason for difficulty in storing fractional numbers
in floating-point representation.
Notice the trailing
9 digit, similar to the trailing 3 digit in the attempted decimal
representation of 1/3 (.3333 …). This lack of precision is
aggravated by arithmetic operations. Consider what would happen if
you added the decimal representation of 1/3 several times. When you
add .33333 … to .99999 … , the theoretical answer is
1.33333 … 2, but in practice, this answer is not possible.
The sums become imprecise as the values continue.
Likewise, the same process
happens when the following DATA step is executed:
data _null_;
do i=-1 to 1 by .1;
if i=0 then put 'AT ZERO';
end;
run;The AT ZERO message
in the DATA step is never printed because the accumulation of the
imprecise number introduces enough error that the exact value of 0
is never encountered. The number is close, but never exactly 0.
This problem is easily resolved by explicitly rounding with each iteration,
as the following statements illustrate:
data _null_;
i=-1;
do while(i<=1);
i=round(i+.1,.001);
if i=0 then put 'AT ZERO';
end;
run;Numeric Comparison Considerations
As discussed in Computational Considerations of Fractions, imprecision can cause problems with computations. Imprecision
can also cause problems with comparisons. Consider the following
example in which the PUT statement is not executed:
data _null_; x=1/3; if x=.33333 then put 'MATCH'; run;
Storing Numbers with Less Precision
As discussed in How SAS Stores Numeric Values, SAS enables numeric values to be
stored on disk with less than full precision. Use the LENGTH statement
to control the number of bytes that are used to store the floating-point
number. Use the LENGTH statement carefully to avoid significant data
loss.
For example, the IBM
mainframe representation uses 8 bytes for full precision, but you
can store as few as 2 bytes on disk. The value 1 is represented as
41 10 00 00 00 00 00 00 in 8 bytes. In 2 bytes, it would be truncated
to 41 10. You still have the full range of magnitude because the
exponent remains intact; there are simply fewer digits involved.
A decrease in the number of digits means either fewer digits to the
right of the decimal place or fewer digits to the left of the decimal
place before trailing zeros must be used.
For example, consider
the number 1234567890, which would be .1234567890 to the 10th power
of 10 (in base 10). If you have only five digits of precision, the
number becomes 123460000 (rounding up). Note that this is the case
regardless of the power of 10 that is used (.12346, 12.346, .0000012346,
and so on).
The only reason to truncate
length by using the LENGTH statement is to save disk space. All values
are expanded to full size to perform computations in DATA and PROC
steps. In addition, you must be careful in your choice of lengths,
as the previous discussion shows.
Consider a length of
2 bytes on an IBM mainframe system. This value enables 1 byte to
store the exponent and sign, and 1 byte for the mantissa. The largest
value that can be stored in 1 byte is 255. Therefore, if the exponent
is 0 (meaning 16 to the 0th power, or 1 multiplied by the mantissa),
then the largest integer that can be stored with complete certainty
is 255. However, some larger integers can be stored because they
are multiples of 16. For example, consider the 8-byte representation
of the numbers 256 to 272 in the following table:
The numbers from 257
to 271 cannot be stored exactly in the first 2 bytes; a third byte
is needed to store the number precisely. As a result, the following
code produces misleading results:
data temp; length x 2; x=257; y1=x+1; run; data _null_; set temp; if x=257 then put 'FOUND'; y2=x+1; run;
The PUT statement is
never executed because the value of X is actually 256 (the value 257
truncated to 2 bytes). Recall that 256 is stored in 2 bytes as 4310,
but 257 is also stored in 2 bytes as 4310, with the third byte of
10 truncated.
You receive no warning
that the value of 257 is truncated in the first DATA step. Note,
however, that Y1 has the value 258 because the values of X are kept
in full, 8-byte floating-point representation in the program data
vector. The value is truncated only when stored in a SAS data set.
Y2 has the value 257, because X is truncated before the number is
read into the program data vector.
Truncating Numbers and Making Comparisons
The TRUNC function truncates a number to a requested
length and then expands the number back to full length. The truncation
and subsequent expansion duplicate the effect of storing numbers in
less than full length and then reading them. For example, if the
variable
x=1/3;is stored with a length of 3, then the following comparison is not true:
if x=1/3 then ...;However, adding the TRUNC function makes the comparison true, as in the following:
if x=trunc(1/3,3) then ...;
Determining How Many Bytes Are Needed to Store a Number Accurately
To determine the minimum
number of bytes needed to store a value accurately, you can use the
TRUNC function. For example, the following program finds the minimum
length of bytes (MINLEN) needed for numbers stored in a native SAS
data set named NUMBERS. The data set NUMBERS contains the variable
VALUE. VALUE contains a range of numbers, in this example, from 269
to 272:
data numbers;
input value;
datalines;
269
270
271
272
;
data temp;
set numbers;
x=value;
do L=8 to 1 by -1;
if x NE trunc(x,L) then
do;
minlen=L+1;
output;
return;
end;
end;
run;
proc print noobs;
var value minlen;
run;Note that the minimum
length required for the value 271 is greater than the minimum required
for the value 272. This fact illustrates that it is possible for
the largest number in a range of numbers to require fewer bytes of
storage than a smaller number. If precision is needed for all numbers
in a range, you should obtain the minimum length for all the numbers,
not just the largest one.
Double-Precision versus Single-Precision Floating-Point Numbers
You might have data created by an external program
that you want to read into a SAS data set. If the data is in floating-point
representation, you can use the RBw.d informat to read in the data.
However, there are exceptions.
The RBw.d informat might
truncate double-precision floating-point numbers if the w value is
less than the size of the double-precision floating-point number (8
on all the operating systems discussed in this section). Therefore,
the RB8. informat corresponds to a full 8-byte floating point. The
RB4. informat corresponds to an 8-byte floating point truncated to
4 bytes, exactly the same as a LENGTH 4 in the DATA step.
An 8-byte floating point
that is truncated to 4 bytes might not be the same as float in a C
program. In the C language, an 8-byte floating-point number is called
a double. In Fortran, it is a REAL*8. In IBM PL/I, it is a FLOAT
BINARY(53). A 4-byte floating-point number is called a float in the
C language, REAL*4 in Fortran, and FLOAT BINARY(21) in IBM PL/I.
On the IBM mainframes,
a single-precision floating-point number is exactly the same as a
double-precision number truncated to 4 bytes. On operating systems
that use the IEEE standard, this is not the case; a single-precision
floating-point number uses a different number of bits for its exponent
and uses a different bias, so that reading in values using the RB4.
informat does not produce the expected results.
Transferring Data between Operating Systems
The problems of
precision and magnitude when you use floating-point numbers are not
confined to a single operating system. Additional problems can arise
when you move from one operating system to another, unless you use
caution. This section discusses factors to consider when you are
transporting data sets with very large or very small numeric values
by using the UPLOAD and DOWNLOAD procedures, the CPORT and CIMPORT
procedures, or transport engines.
Summary of Floating-Point Numbers Stored in 8 Bytes shows the maximum number of digits of the base, exponent,
and mantissa. Because there are differences in the maximum values
that can be stored in different operating environments, there might
be problems in transferring your floating-point data from one computer
to another.
Consider transporting
data between an IBM mainframe and a PC, for example. The IBM mainframe
has a range limit of approximately .54E−78 to .72E76 (and their
negative equivalents and 0) for its floating-point numbers. Other
computers, such as the PC, have wider limits (the PC has an upper
limit of approximately 1E308). Therefore, if you are transferring
numbers in the magnitude of 1E100 from a PC to a mainframe, you lose
that magnitude. During data transfer, the number is set to the minimum
or maximum allowable on that operating system, so 1E100 on a PC is
converted to a value that is approximately .72E76 on an IBM mainframe.
CAUTION:
Transfer
of data between computers can affect numeric precision.
If you are transferring data from an IBM mainframe to a PC, notice
that the number of bits for the mantissa is 4 less than that for an
IBM mainframe, which means you lose 4 bits when moving to a PC. This
precision and magnitude difference is a factor when moving from one
operating environment to any other where the floating-point representation
is different.