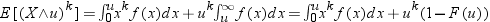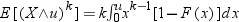LIMMOMENT Function
Computes the limited moment of any distribution
for which you have defined a cumulative distribution function (CDF).
| Category: | Special Purpose Functions |
| Notes: | LIMMOMENT is a special purpose function that is automatically
provided by the FCMP procedure for your convenience.
If you specify order k and upper limit u, then the LIMMOMENT function computes the limited moment as E[min(X,u)k], where E denotes an expectation taken over the distribution of a random variable X that is defined by the specified CDF function. |
Syntax
imom=LIMMOMENT('CDF-function-name', options-array, order, limit,
parameter-1,
parameter-2, parameter-n);
Required Arguments
- 'CDF-function-name'
-
specifies the name of the CDF function. Enclose CDF-function-name in quotation marks.Requirement:CDF-function-name must be a function defined using the FCMP procedure. It must have a signature as follows:
function <CDF-function-name> (x, parameter-1, parameter-2, …, parameter-n);
endsub;
Note:It is recommended that the CDF be a continuous function. For discrete CDF, the LIMMOMENT function might not be able to compute the limited moment.
- options-array
-
specifies an array of options to use with the LIMMOMENT function. Options-array is used to control and monitor the process of numerical integration employed to compute the limited amount. Options-array can be a missing value (.), or it can have up to four of the following elements in the following order:
- desired-accuracy
-
specifies the desired accuracy of the numerical integration. You can specify any value in the range (0,0.1). If you specify a smaller value, the result is a more accurate estimate of the moment, but it takes longer to compute the desired-accuracy. The default for desired-accuracy is 1.0e-8.
- initial-step-size
-
specifies the step size that is used initially by the numerical integration process. An increase in the value results in a linear decrease in the number of times the integrand is evaluated. Typically, using the default value of 1 produces good results. The default for initial-step-size is 1.
- maximum-iterations
-
specifies the maximum number of iterations that are used to refine the integration result in order to achieve the desired accuracy. An increase in this value results in an exponential increase in the number of times the integrand is evaluated. The default value for maximum-iterations is 8.
- return-code
-
specifies the return status. If options-array is of dimension 4 or more, then the fourth element contains the return status. Return-code can have one of the following values:
Details
Let a random variable X have
a probability distribution with probability density function f(x;θ) and
cumulative distribution function F(x;θ),
where θ denotes the parameters of the distribution. For a specified
upper limit u, the kth–order
limited moment of this distribution is defined as follows:
Because the expression
needs only F(x), you need to
specify only the CDF function for the distribution. Limited moments
are often used in insurance applications to compute the maximum amount
expected to be paid if the policy limit is set at a certain value.
Example: Computing a Limited Moment for a Lognormal Distribution
This example demonstrates
how you can compute the limited moment for any parametric distribution
in a DATA step using the LIMMOMENT function. The example uses the
lognormal distribution for illustration, but it can be extended to
any distribution for which you can programmatically define a CDF function.
The following statements define an FCMP function LOGN_LIMMOMENT that
uses the LIMMOMENT function and the CDF function to compute limited
moments from the lognormal distribution:
proc fcmp library=work.mycdf outlib=work.mylimmom.functions; function logn_limmoment(order, limit, mu, sigma, rc); outargs rc; array opts[4] / nosym (1.0e-8 . . .); m = limmoment("logn_cdf", opts, order, limit, mu, sigma); rc = opts[4]; /* return code */ return (m); endsub; quit;
The preceding code assumes
that you have stored the definition of the LOGN_CDF function in an
FCMP library called Work.Mycdf using a PROC FCMP step as follows:
proc fcmp outlib=work.mycdf.functions;
function logn_cdf(x, Mu, Sigma);
if (x >= constant('MACEPS')) then do;
z = (log(x) - Mu)/Sigma;
return (CDF('NORMAL', z));
end;
return (0);
endsub;
quit;