INVCDF Function
Computes the quantile from any distribution for
which you have defined a cumulative distribution function (CDF).
| Category: | Special Purpose Functions |
| Notes: | INVCDF is a special purpose function that is automatically
provided by the FCMP procedure for your convenience.
If you specify a probability p for
a distribution with CDF denoted by |
Syntax
quantile=INVCDF('CDF-function-name', options-array, cumulative-probability,
parameter-1,
parameter-2, ..., parameter-n);
Required Arguments
- 'CDF-function-name'
-
specifies the name of the CDF function. Enclose CDF-function-name in quotation marks.Requirement:CDF-function-name must be a function defined using the FCMP procedure. It must have a signature as follows:
function <CDF-function-name> (x, parameter-1, parameter-2, …, parameter-n);
endsub;
Note:It is recommended that the CDF be a continuous function. For discrete CDF, the INVCDF function might not be able to compute the quantile.
- options-array
-
specifies an array of options to use with the INVCDF function. Options-array is used to control and monitor the process of inverting the CDF. Options-array can be a missing value (.), or it can have up to four of the following elements in the following order:
- initial-value
-
specifies the initial guess for the quantile at which the inversion process starts. This is useful when you have an idea of the approximate value for quantile (for example, from the empirical estimate of the CDF). The default for initial-value is 0.1.
- desired-accuracy
-
specifies the desired relative accuracy of the quantile. You can specify any value in the range (0,0.1). If you specify a smaller value, the result is a more accurate estimate of the quantile, but it might take longer to invert the CDF. The default for desired-accuracy is 1.0e-8.
- domain-type
-
specifies the domain for the CDF function. A missing value or a value of 0 indicates a nonnegative support, that is [0,∞). Any other value indicates a support over the entire real line, that is
(-∞,∞) . The default for domain-type is 0.
- return-code
-
specifies the return status. If options-array is of dimension 4 or more, then the fourth element contains the return status. Return-code can have one of the following values:
Details
The INVCDF function
finds the quantile for the specified cumulative probability from a
distribution whose cumulative distribution function is specified by
the CDF-function-name argument.
In other words, it inverts the CDF function such that the following
expression is true:
cumulative-probability = CDF-function-name(quantile,<parameters>)
If  denotes the desired accuracy of the quantile for
cumulative probability p, then
INVCDF attempts to compute the quantile q such
that
denotes the desired accuracy of the quantile for
cumulative probability p, then
INVCDF attempts to compute the quantile q such
that 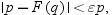 where F(x) denotes
the CDF evaluated at x.
where F(x) denotes
the CDF evaluated at x.
 denotes the desired accuracy of the quantile for
cumulative probability p, then
INVCDF attempts to compute the quantile q such
that
denotes the desired accuracy of the quantile for
cumulative probability p, then
INVCDF attempts to compute the quantile q such
that 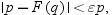 where F(x) denotes
the CDF evaluated at x.
where F(x) denotes
the CDF evaluated at x.
Comparisons
You can regard this
function as a generic extension of the QUANTILE function, which computes
quantiles only from specific distributions. The INVCDF function enables
you to compute quantiles from any continuous distribution as long
as you can programmatically define that distribution’s CDF
function. Unlike the QUANTILE function, this function cannot be used
directly in a DATA step. It can only be used inside the definition
of an FCMP function or subroutine. However, this is not a limitation
because you can invoke the FCMP function that uses it from a DATA
step. See the following example.
Example: Generating a Random Sample from an Exponential Distribution
The following example
demonstrates how you can generate a random sample from any parametric
distribution in a DATA step using the INVCDF function. The example
uses the exponential distribution for illustration, but it can be
extended to any distribution for which you can programmatically define
a CDF function. The following statements define an FCMP function EXP_QUANTILE
that uses the INVCDF function and the CDF function to compute a quantile
from the exponential distribution.
proc fcmp library=work.mycdf outlib=work.myquantile.functions; function exp_quantile(cdf, theta, rc); outargs rc; array opts[4] / nosym(0.1 1.0e-8 .); q=invcdf("exp_cdf", opts, cdf, theta); rc=opts[4]; /* return code */ return(q); endsub; quit;
The preceding code assumes
that you have stored the definition of the EXP_CDF function in an
FCMP library called Work.Mycdf using a PROC FCMP step as follows:
proc fcmp outlib=work.mycdf.functions;
function exp_cdf(x, theta);
return(1.0 - exp(-x/Theta));
endsub;
quit;Now you can invoke the
EXP_QUANTILE function from a DATA step to generate a random sample
from the exponential distribution with a scale parameter (theta) that
has a value of 50. Note that the locations of the EXP_CDF and the
EXP_QUANTILE functions need to be specified with the appropriate value
for the CMPLIB= option before you execute the DATA step: