Short Run Process Control
See SHWSRUN in the SAS/QC Sample LibraryWhen conventional Shewhart charts are used to establish statistical control, the initial control limits are typically based on 25 to 30 subgroup samples. Often, however, this amount of data is not available in manufacturing situations where product changeover occurs frequently or production runs are limited.
A variety of methods have been introduced for analyzing data from a process that is alternating between short runs of multiple products. The methods commonly used in the United States are variations of two basic approaches:[106]
-
the difference from nominal approach. A product-specific nominal value is subtracted from each measured value, and the differences (together with appropriate control limits) are charted. Here it is assumed that the nominal value represents the central location of the process (ideally estimated with historical data) and that the process variability is constant across products.
-
the standardization approach. Each measured value is standardized with a product-specific nominal and standard deviation values. This approach is followed when the process variability is not constant across products.
These approaches are highlighted in this section because of their popularity, but two alternatives that are technically more sophisticated are worth noting.
-
Hillier (1969) provided a method for modifying the usual control limits for
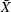and R charts in startup situations where fewer than 25 subgroup samples are available for estimating the process mean 
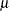and standard deviation 
; also refer to Quesenberry (1993).
-
Quesenberry (1991b, 1991a) introduced the so-called Q chart for short (or long) production runs, which standardizes and normalizes the data using probability integral transformations.
SAS examples illustrating these alternatives are provided in the SAS/QC sample library and are described by Rodriguez and Bynum (1992).