OUTPUT Statement :: SAS/QC(R) 13.1 User's Guide

OUTPUT Statement

OUTPUT OUT= SAS-data-set <options> ;

You use the OUTPUT statement to save a design in an output data set. Optionally, you can use the OUTPUT statement to modify the design by specifying values to be output for factors, creating new factors, randomizing the design, and replicating the design. You specify the output data set as follows:

OUT=SAS-data-set

gives the name of the output data set in which the design is saved. Note that OUT= is required.

options

You can use the options to

recode the values for design factors
recode the values for the block variable
replicate the entire design
replicate each point of the design
randomize the design
create derived factors based on the original factors

The following list describes the preceding options:

Recode Design Factors

By default, the output data set contains a variable for each factor in the design coded with standard values, as follows:

For factors with 2 levels (q = 2), the values are –1 and +1.
For factors with 3 levels (q = 3), the values are –1, 0, and +1.
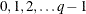For factors with q levels (q > 3), the values are $0, 1, 2, \ldots q-1$ .

You can recode the levels of the factor from the standard levels to levels appropriate for your situation.

For example, suppose that you want to recode a three-level factorial design from the standard levels –1, 0, and +1 to the actual levels. Suppose the factors are pressure (Pressure) with character levels, agitation rate (Rate) with numeric levels, and temperature (Temperature) with numeric levels. You can use the following statement to recode the factor levels and save the design in a SAS data set named RECODE:

output out=recode Pressure    cvals=('low' 'medium' 'high')
                  Rate        nvals=(20   40  60)
                  Temperature cvals=(100 150 200);

The general form of options to recode factors is as follows:

factor-name NVALS= (level1 level2 …levelq)

factor-name CVALS=('level1' 'level2' …'levelq')

where

factor-name: gives the name of the design factor.
NVALS=: lists new numeric levels for design factors.
CVALS=: lists new character levels for design factors. Each string can be up to 40 characters long.

When recoding a factor, the NVALS= and CVALS= options map the first value listed to the lowest value for the factor, the second value listed to the next lowest value, and so on. If you rename and recode a factor, the type and length of the new variable are determined by whether you use the CVALS= option (character variable with length equal to the longest string) or the NVALS= option (numeric variable). For more information about recoding a factor, see Factor Variable Characteristics in the Output Data Set.

Recode Block Factor

If the design uses blocking, the output data set automatically contains a block variable named BLOCK, and for a design with b blocks, the default values of the block variable are $1, 2, \ldots b$ . You can rename the block variable and optionally recode the block levels from the default levels to levels appropriate for your situation.

For example, for a design arranged in four blocks, suppose that the block variable is the day of the week (Day) and that the four block levels of character type are Mon, Tue, Wed, and Thu. You can use the following statement to rename the block variable, recode the block levels, and save the design in a SAS data set named RECODE:

output out=recode blockname=Day cvals=('Mon''Tue''Wed''Thu');

The general form of options to change the block variable name or change the block levels is as follows:

BLOCKNAME= block-name <NVALS= (level1 level2 …levelb)>

BLOCKNAME= block-name <CVALS= ('level1' 'level2' …'levelb')>

where

block-name: gives a new name for the block factor.
NVALS=: lists new numeric levels for the block factor. For details, see the section Recode Design Factors.
CVALS=: lists new character levels for the block factor. For details, see the section Recode Design Factors.

Note that you can simply rename the block variable by using only the BLOCKNAME= option, without using the NVALS= and CVALS= options.

Replicate Entire Design

DESIGNREP=c DESIGNREP=SAS-data-set

replicates the entire design. Specify DESIGNREP=c to replicate the design c times, where c is an integer. Alternatively, you can specify a SAS data set with the DESIGNREP option. In this case, the design is replicated once for each point in the DESIGNREP= data set, and the OUT= data set contains the variables in the DESIGNREP= data set in addition to the design variables.

In mathematical notation, the OUT= data set is the direct product of the DESIGNREP= data set and the design. If the design is a and the DESIGNREP= data set is b, then the OUT= data set is b $\otimes$ a, where $\otimes$ denotes the direct product.

For details, see the section Replication. For illustrations of the difference between the DESIGNREP= and POINTREP= options, see Example 7.6 and Example 7.7.

Replicate Design Point

POINTREP=p POINTREP=SAS-data-set

replicates each point of the design. Specify POINTREP=p to replicate each design point p times, where p is an integer. Alternatively, you can specify a SAS data set with the POINTREP= option. In this case, the POINTREP= data set is replicated once for each point in the design and the OUT= data set contains the variables in the POINTREP= data set in addition to the design variables.

In mathematical notation, the OUT= data set is the direct product of the design and the POINT= data set. If the design is a and the POINTREP= data set is b, then the OUT= data set is a $\otimes$ b, where $\otimes$ denotes the direct product.

For details, see the section Replication. For illustrations of the difference between the DESIGNREP= and POINTREP= options, see Example 7.6 and Example 7.7.

Randomize Design

RANDOMIZE <(u)> <NOVALRAN>

randomizes the design. See the section Randomization for details. The following options are available:

(u)

specifies an integer used to start the pseudo-random number generator for randomizing the design. The value of u must be enclosed in parentheses immediately after the keyword RANDOMIZE. If you do not specify a seed, or if you specify a value less than or equal to zero, by default the seed is generated from reading the time of day from the computer’s clock.

NOVALRAN

prevents the randomization of theoretical factor levels to actual levels. The randomization of run order is still performed.

Create Derived Factors

You can create derived factors based on the joint values of a set of the design factors. Each distinct combination of levels of the design factors corresponds to a single level for the derived factor. Thus, when you create a derived factor from k design factors, each with q levels, the derived factor has $q^ k$ levels. Derived factors are useful when you create mixed-level designs; see Example 7.8 for an example. See the section Structure of General Factorial Designs for information about how the levels of design factors are mapped into levels of the derived factor. The general form of the option for creating derived factors is

[ design-factors]= derived-factor <NVALS= (list-of-numbers)>

[ design-factors]= derived-factor <CVALS= ('string1' 'string2' …'stringn')>

where

design-factors: gives names of factors currently in the design. These factors are combined to create the new derived factor.
derived-factor: gives a name to the new derived factor. This name must not be used in the design.
NVALS=: lists new numeric levels for the derived factor.
CVALS=: lists new character levels for the derived factor. See the section Recode Design Factors for details.

If you create a derived factor and do not use the NVALS= or CVALS= option to assign levels to the derived factor, the FACTEX procedure assigns the values $0,~ 1, \ldots , q^ k-1$ , where the derived factor is created from k design factors, each with q levels. In general, the CVALS= or NVALS= list for a derived factor must contain $q^ k$ values.

The following statement gives an example of creating a derived factor and then renaming the levels of the factor:

output out=new [A1 A2]=A cvals=('A' 'B' 'C' 'D');

This statement converts two 2-level factors (A1 and A2) into one 4-level factor (A), which has the levels A, B, C, and D.