Functions

ATI2 Function

Subsections:

computes the average total inspection for a double-sampling plan.

Syntax

ATI2($N,a_{1},r_{1},a_{2},n_{1},n_{2},p$)

where

N

is the lot size, where $N\geq 2$.

$a_{1}$

is the acceptance number for the first sample, where $a_{1}\geq 0$.

$r_{1}$

is the rejection number for the first sample, where $r_{1}>a_{1}+1$.

$a_{2}$

is the acceptance number for the second sample, where $a_{2}\geq a_{1}$.

$n_{1}$

is the size of the first sample, where $n_{1}\geq 1$ and $n_{1}+n_{2}\leq N$.

$n_{2}$

is the size of the second sample, where $n_{2}\geq 1$ and $n_{1}+n_{2}\leq N$.

p

is the proportion of nonconforming items produced by the process, where 0 < p < 1.

Description

The ATI2 function returns the average total inspection for a Type B double-sampling plan. For details on Type B double-sampling plans, see Types of Sampling Plans.

The average total inspection is

\[ \mbox{ATI}=n_1P_{a_1}+(n_1+n_2)P_{a_2}+N(1-P_{a_1}-P_{a_2}) \]

where

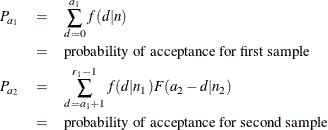
\begin{eqnarray*} P_{a_{1}} & = & \sum _{d=0}^{a_{1}} f(d|n) \\ & = & \mbox{probability of acceptance for first sample} \\ P_{a_{2}} & = & \sum _{d=a_{1}+1}^{r_{1}-1} f(d|n_{1})F(a_{2}-d|n_{2}) \\ & = & \mbox{probability of acceptance for second sample} \end{eqnarray*}

and

\begin{eqnarray*} f(d|n) & = & (\stackrel{n}{_ d})p^{d}(1-p)^{n-d} \\ & = & \mbox{binomial probability that the number of nonconforming items }\\ & & \mbox{in a sample of size } n \mbox{ is exactly } d \\ F(a|n) & = & \sum _{d=0}^{a}f(d|n) \\ & = & \mbox{probability that the number of nonconforming items is less} \\ & & \mbox{than or equal to } a \end{eqnarray*}

Examples

The following statements result in a value of 110.35046381: 

data;
   ati=ati2(120,0,2,1,13,13,0.18);
   put ati;
run;