The OPTEX Procedure

GENERATE Statement

  • GENERATE <options>;

You use the GENERATE statement to customize the search for a design. By default, the OPTEX procedure searches for a design as follows:

  • using the exchange algorithm (METHOD=EXCHANGE)

  • using D-optimality as the optimality criterion (CRITERION=D)

  • using a completely random initial design to start the search (INITDESIGN=RANDOM)

  • selecting candidate points only from the DATA= data set (modified by using AUGMENT= or INITDESIGN= data sets)

  • performing 10 iterations in the search (ITER=10)

  • finding a design with 10 + p points, where p is the number of parameters in the model (modified by using the N= or INITDESIGN= option)

The following options can be used to modify these defaults:

AUGMENT=SAS-data-set

specifies a data set that contains a design to be augmented—in other words, a set of points that must be contained in the design generated. When creating designs, the OPTEX procedure adds points from the DATA= data set (or the last data set created, if DATA= is not specified) to points from the AUGMENT= data set. The number of points in the design to be augmented must be less than the number of points specified with the N= option. For details, see the section AUGMENT= Data Set.

CRITERION=crit

specifies the optimality criterion used in the search. You can specify any one of the following:

CRITERION=D

specifies D-optimality; the optimal design maximizes the determinant 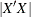$|X’X|$ of the information matrix for the design. This is the default criterion.

CRITERION=A

specifies A-optimality; the optimal design minimizes the sum of the variances of the estimated parameters for the model, which is the same as minimizing the trace of $(X’X)^{-1}$.

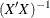CRITERION=U

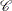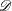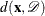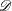specifies U-optimality; the optimal design minimizes the sum of the minimum distances from each candidate point to the design. That is, if $\mc{C}$ is the set of candidate points, $\mc{D}$ is the set of design points, and $d(\mb{x},\mc{D})$ is the minimum distance from $\mb{x}$ to any point in $\mc{D}$, then a U-optimal design minimizes

\[ \sum _{\Strong{x}\in \mc{C}} d(\Strong{x},\mc{D}) \]

This measures how well the design "covers" the candidate set; thus, a U-optimal design is also called a uniform coverage design.

CRITERION=S

specifies S-optimality; the optimal design maximizes the harmonic mean of the minimum distance from each design point to any other design point. Mathematically, an S-optimal design maximizes

\[ \frac{N_ D}{\sum _{\Strong{y}\in \mc{D}} 1/d(\Strong{y},\mc{D}-\Strong{y})} \]

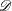where $\mc{D}$ is the set of design points, and 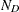$N_ D$ is the number of points in 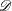$\mc{D}$. This measures how spread out the design points are; thus, an S-optimal design is also called a maximum spread design.

For more information on the different criteria, see the section Optimality Criteria.

INITDESIGN=initialization-method

specifies a method of obtaining an initial design for the search procedure. Valid values of initialization-method are as follows:

SEQUENTIAL

specifies an initial design chosen by a sequential search. The design given by INITDESIGN=SEQUENTIAL is the same as the design given by METHOD=SEQUENTIAL. You can use the INITDESIGN=SEQUENTIAL option with other values of the METHOD= option to specify a sequential design as the initial design for various search methods. For details, see Search Methods.

RANDOM

specifies a completely random initial design. The initial design generated consists of a random selection of observations from the DATA= data set.

PARTIAL<(m )>

specifies an initial design by using a mixture of RANDOM and SEQUENTIAL methods. A small number 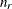$n_ r$ of points for the initial design are chosen at random from the candidates, and the rest of the design points are chosen by a sequential search. (For a definition of the sequential search, see the section Search Methods.)

You can specify the optional integer m to modify the selection of 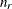$n_ r$. By default, or if m = 0, 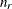$n_ r$ is randomly chosen between 0 and one less than half the number of parameters in the linear model. If m > 0, then 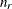$n_ r$ is randomly chosen between 0 and m for each try. If m < 0, then 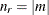$n_ r=|m|$ for each try. The maximum value for 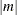$|m|$ is the number of points in the design. Refer to Galil and Kiefer (1980) for notes on choosing $n_ r$.

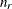SAS-data-set

specifies a data set that holds the initial design. Use this initialization-method when you have a specific design that you want to improve or when you want to evaluate an existing design. For details, see INITDESIGN= Data Set.

The default initialization method depends on the search procedure as shown in Table 14.6.

Table 14.6: Default Initialization Methods

Search Procedure

Default Initialization Method

(METHOD= option)

(INITDESIGN= option)

DETMAX

PARTIAL

EXCHANGE

RANDOM

FEDOROV

RANDOM

M_FEDOROV

PARTIAL

SEQUENTIAL

none


If you specify INITDESIGN=SAS-data-set and METHOD=SEQUENTIAL, no search is performed; the INITDESIGN= data set is taken as the final design. By specifying these options, you can use the procedure to evaluate an existing design.

ITER=n

specifies the number n of searches to make. Because local optima are common in difficult search problems, it is often a good idea to make several tries for the optimal design with a random or partially random method of initialization (see the preceding INITDESIGN= option). By default, n = 10.

The n designs found are sorted by their respective efficiencies according to the current optimality criterion (see the CRITERION= option.) The most efficient design is assigned a design-number of 1, the second most efficient design is assigned a design-number of 2, and so on. You can then use the design-number in the EXAMINE and OUTPUT statements to display the characteristics of a design or to save a design in a data set.

KEEP=m

specifies that only the best m designs are to be retained. The value m must be less than or equal to the value n of the ITER= option. By default m = n, so that all iterations are kept. This option is useful when you want to make many searches to overcome the problem of local optima but are interested only in the results of the best m designs.

METHOD=DETMAX<(level)>
METHOD=EXCHANGE <(k)>
METHOD=FEDOROV
METHOD=M_FEDOROV
METHOD=SEQUENTIAL

specifies the procedure used to search for the optimal design. The default is METHOD=EXCHANGE.

With METHOD=DETMAX, the optional level gives the maximum excursion level for the search, where level is an integer greater than or equal to 1. Enclose the value of level in parentheses immediately following the word DETMAX. The default value for level is 4. In general, larger values of level result in longer search times.

When METHOD=EXCHANGE, the optional k specifies the k-exchange search method of Johnson and Nachtsheim (1983), which generalizes the modified Fedorov search algorithm of Cook and Nachtsheim (1980). Enclose the value of k in parentheses immediately following the word EXCHANGE.

From fastest to slowest, the methods are

SEQUENTIAL $\rightarrow $ EXCHANGE $\rightarrow $ DETMAX $\rightarrow $ M_FEDOROV $\rightarrow $ FEDOROV

In general, slower methods result in more efficient designs. While the default method EXCHANGE always works relatively quickly, you might want to specify a more reliable method, such as M_FEDOROV, with fast computers or small to moderately sized problems.

See the section Search Methods for details on the algorithms.

N=n
N=SATURATED

specifies the number of points in the final design. The default design size is 10 + p, where p is the number of parameters in the model. If you use the INITDESIGN= option, the default number is the number of points in the initial design. Specify N=n to search for a design with n points. Specify N=SATURATED to search for a design with the same number of points as there are parameters in the model. A saturated design has no degrees of freedom to estimate error and should be used with caution.