The KRIGE2D Procedure
Ordinary Kriging
Denote the SRF by ![]() . Following the notation in Cressie (1993), the following model for
. Following the notation in Cressie (1993), the following model for ![]() is assumed:
is assumed:
|
|
Here, ![]() is the fixed, unknown mean of the process, and
is the fixed, unknown mean of the process, and ![]() is a zero mean SRF, which represents the variation around the mean.
is a zero mean SRF, which represents the variation around the mean.
In most practical applications, an additional assumption is required in order to estimate the covariance ![]() of the
of the ![]() process. This assumption is second-order stationarity:
process. This assumption is second-order stationarity:
|
|
This requirement can be relaxed slightly when you are using the semivariogram instead of the covariance. In this case, second-order
stationarity is required of the differences ![]() rather than
rather than ![]() :
:
|
|
By performing local kriging, the spatial processes represented by the previous equation for ![]() are more general than they appear. In local kriging, at an unsampled location
are more general than they appear. In local kriging, at an unsampled location ![]() , a separate model is fit using only data in a neighborhood of
, a separate model is fit using only data in a neighborhood of ![]() . This has the effect of fitting a separate mean
. This has the effect of fitting a separate mean ![]() at each point, and it is similar to the kriging with trend (KT) method discussed in Journel and Rossi (1989).
at each point, and it is similar to the kriging with trend (KT) method discussed in Journel and Rossi (1989).
Given the N measurements ![]() at known locations
at known locations ![]() , you want to obtain a prediction of Z at an unsampled location
, you want to obtain a prediction of Z at an unsampled location ![]() . When the following three requirements are imposed on the predictor
. When the following three requirements are imposed on the predictor ![]() , the OK predictor is obtained:
, the OK predictor is obtained:
-
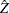 is linear in
is linear in 
-
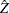 is unbiased
is unbiased
-
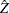 minimizes the mean square prediction error
minimizes the mean square prediction error ![$\mr {E}[(Z(\bm {s}_0)-\hat{Z}(\bm {s}_0))^2]$](images/statug_krige2d0172.png)
Linearity requires the following form for ![]() :
:
|
|
Applying the unbiasedness condition to the preceding equation yields
|
|
Finally, the third condition requires a constrained linear optimization that involves ![]() and a Lagrange parameter
and a Lagrange parameter ![]() . This constrained linear optimization can be expressed in terms of the function
. This constrained linear optimization can be expressed in terms of the function ![]() given by
given by
![\[ L = \mr {E} \left[ \left( Z(\bm {s}_0) - \sum _{i=1}^{N}\lambda _ iZ(\bm {s}_ i) \right)^2 \right] - 2m\left(\sum _{i=1}^{N}\lambda _ i-1 \right) \]](images/statug_krige2d0180.png) |
Define the ![]() column vector
column vector ![]() by
by
|
|
and the ![]() column vector
column vector ![]() by
by
|
|
The optimization is performed by solving
|
|
in terms of ![]() and m.
and m.
The resulting matrix equation can be expressed in terms of either the covariance ![]() or semivariogram
or semivariogram ![]() . In terms of the covariance, the preceding equation results in the matrix equation
. In terms of the covariance, the preceding equation results in the matrix equation
|
|
where
![\[ \mb {C} = \left( \begin{array}{ccccc} C_ z(\bm {0}) & C_ z(\bm {s}_1-\bm {s}_2) & \cdots & C_ z(\bm {s}_1-\bm {s}_ N) & 1 \\ C_ z(\bm {s}_2-\bm {s}_1) & C_ z(\bm {0}) & \cdots & C_ z(\bm {s}_2-\bm {s}_ N) & 1 \\ & & \ddots & & \\ C_ z(\bm {s}_ N-\bm {s}_1) & C_ z(\bm {s}_ N-\bm {s}_2) & \cdots & C_ z(\bm {0}) & 1 \\ 1 & 1 & \cdots & 1 & 0 \\ \end{array} \right) \]](images/statug_krige2d0192.png) |
and
![\[ \mb {C_0} = \left( \begin{array}{c} C_ z(\bm {s}_0-\bm {s}_1) \\ C_ z(\bm {s}_0-\bm {s}_2) \\ \vdots \\ C_ z(\bm {s}_0-\bm {s}_ N) \\ 1 \\ \end{array} \right) \]](images/statug_krige2d0193.png) |
The solution to the previous matrix equation is
|
|
Using this solution for ![]() and m, the ordinary kriging prediction at
and m, the ordinary kriging prediction at ![]() is
is
|
|
with associated prediction error the square root of the variance
|
|
where ![]() is
is ![]() with the 1 in the last row removed, making it an
with the 1 in the last row removed, making it an ![]() vector.
vector.
These formulas are used in the best linear unbiased prediction (BLUP) of random variables (Robinson 1991). Further details are provided in Cressie (1993, pp. 119–123).
Because of possible numeric problems when solving the previous matrix equation, Deutsch and Journel (1992) suggest replacing the last row and column of 1s in the preceding matrix ![]() by
by ![]() , keeping the 0 in the
, keeping the 0 in the ![]() position and similarly replacing the last element in the preceding right-hand vector
position and similarly replacing the last element in the preceding right-hand vector ![]() with
with ![]() . This results in an equivalent system but avoids numeric problems when
. This results in an equivalent system but avoids numeric problems when ![]() is large or small relative to 1.
is large or small relative to 1.
