The SURVEYLOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
 PROC SURVEYLOGISTIC StatementBY StatementCLASS StatementCLUSTER StatementCONTRAST StatementDOMAIN StatementEFFECT StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement
PROC SURVEYLOGISTIC StatementBY StatementCLASS StatementCLUSTER StatementCONTRAST StatementDOMAIN StatementEFFECT StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement -
Details
 Missing ValuesModel SpecificationModel FittingSurvey Design InformationLogistic Regression Models and ParametersVariance EstimationDomain AnalysisHypothesis Testing and EstimationLinear Predictor, Predicted Probability, and Confidence LimitsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
Missing ValuesModel SpecificationModel FittingSurvey Design InformationLogistic Regression Models and ParametersVariance EstimationDomain AnalysisHypothesis Testing and EstimationLinear Predictor, Predicted Probability, and Confidence LimitsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Notation
Let Y be the response variable with categories ![]() . The p covariates are denoted by a p-dimension row vector
. The p covariates are denoted by a p-dimension row vector ![]() .
.
For a stratified clustered sample design, each observation is represented by a row vector, ![]() , where
, where
-
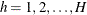 is the stratum index
is the stratum index
-
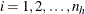 is the cluster index within stratum h
is the cluster index within stratum h
-
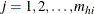 is the unit index within cluster i of stratum h
is the unit index within cluster i of stratum h
-
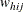 denotes the sampling weight
denotes the sampling weight
-
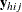 is a D-dimensional column vector whose elements are indicator variables for the first D categories for variable Y. If the response of the jth unit of the ith cluster in stratum h falls in category d, the dth element of the vector is one, and the remaining elements of the vector are zero, where
is a D-dimensional column vector whose elements are indicator variables for the first D categories for variable Y. If the response of the jth unit of the ith cluster in stratum h falls in category d, the dth element of the vector is one, and the remaining elements of the vector are zero, where 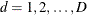 .
.
-
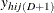 is the indicator variable for the
is the indicator variable for the 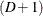 category of variable Y
category of variable Y
-
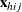 denotes the k-dimensional row vector of explanatory variables for the jth unit of the ith cluster in stratum h. If there is an intercept, then
denotes the k-dimensional row vector of explanatory variables for the jth unit of the ith cluster in stratum h. If there is an intercept, then 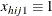 .
.
-
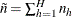 is the total number of clusters in the sample
is the total number of clusters in the sample
-
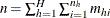 is the total sample size
is the total sample size
The following notations are also used:
-
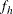 denotes the sampling rate for stratum h
denotes the sampling rate for stratum h
-
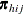 is the expected vector of the response variable:
is the expected vector of the response variable:
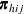
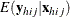

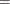
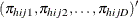
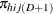
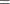
Note that ![]() , where 1 is a D-dimensional column vector whose elements are 1.
, where 1 is a D-dimensional column vector whose elements are 1.