The SURVEYLOGISTIC Procedure
- Overview
- Getting Started
-
Syntax
PROC SURVEYLOGISTIC StatementBY StatementCLASS StatementCLUSTER StatementCONTRAST StatementDOMAIN StatementEFFECT StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementUNITS StatementWEIGHT Statement -
DetailsMissing ValuesModel SpecificationModel FittingSurvey Design InformationLogistic Regression Models and ParametersVariance EstimationDomain AnalysisHypothesis Testing and EstimationLinear Predictor, Predicted Probability, and Confidence LimitsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
-
Examples
- References
Analysis of Maximum Likelihood Estimates
By default, PROC SURVEYLOGISTIC displays the following information in the “Analysis of Maximum Likelihood Estimates” table:
-
the degrees of freedom for Wald chi-square test
-
maximum likelihood estimate of the parameter
-
estimated standard error of the parameter estimate, computed as the square root of the corresponding diagonal element of the estimated covariance matrix
-
Wald chi-square statistic, computed by squaring the ratio of the parameter estimate divided by its standard error estimate
-
p-value of the Wald chi-square statistic with respect to a chi-square distribution with one degree of freedom
-
standardized estimate for the slope parameter, given by
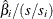, where 
is the total sample standard deviation for the ith explanatory variable and
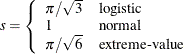
You need to specify the STB option in the MODEL statement to obtain these estimates. Standardized estimates of the intercept parameters are set to missing.
-
value of (e
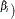for each slope parameter 
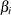if you specify the EXPB option in the MODEL statement. For continuous variables, this is equivalent to the estimated odds
ratio for a one-unit change.
-
label of the variable (if space permits) if you specify the PARMLABEL option in the MODEL statement. Due to constraints on the line size, the variable label might be suppressed in order to display the table in one panel. Use the SAS system option LINESIZE= to specify a larger line size to accommodate variable labels. A shorter line size can break the table into two panels, allowing labels to be displayed.