The SURVEYPHREG Procedure

Contrasts

For a testable hypothesis $H_{0} \colon \mb {L} \bbeta = 0$ , the Wald F statistic is computed as

$F_{\mbox{Wald}} = \frac{(\mb {L}^* \hat{\bbeta }) ({\mb {L}^*} \widehat{\mb {V}} \mb {L}^* )^{-1} (\mb {L}^* \hat{\bbeta }) }{\mbox{rank}(\mb {L}) }$

where $\mb {L}$ is a contrast vector or matrix that you specify, ${\bbeta }$ is the vector of regression parameters, $\hat{\bbeta }$ is the estimated regression coefficients, $\widehat{\mb {V}}$ is the estimated covariance matrix of $\hat{\bbeta }$ , rank( $\mb {L}$ ) is the rank of $\mb {L}$ , and $\mb {L}^*$ is a matrix such that

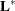$\mb {L}^*$ has the same number of columns as $\mb {L}$
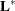$\mb {L}^*$ has full row rank
the rank of 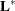$\mb {L}^*$ equals the rank of the $\mb {L}$ matrix
all rows of 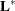$\mb {L}^*$ are estimable functions
the Wald F statistic computed by using the 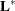$\mb {L}^*$ matrix is equivalent to the Wald F statistic computed by using the $\mb {L}$ matrix with any row deleted that is a linear combination of previous rows

If $\mb {L}$ is a full-rank matrix and all rows of $\mb {L}$ are estimable functions, then $\mb {L}^*$ is the same as $\mb {L}$ . It is possible that $\mb {L}$ matrix cannot be constructed for a given set of linear contrasts, in which case the contrasts are not testable.

If the DF=NONE option in the MODEL statement is specified, then the procedure performs a chi-square significance test.