The FMM Procedure

Model Options

ALPHA=number

requests that confidence intervals be constructed for each of the parameters with confidence level 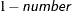$1-\mr {\Argument{number}}$ . The value of number must be between 0 and 1; the default is 0.05.

CL

requests that confidence limits be constructed for each of the parameter estimates. The confidence level is 0.95 by default; this can be changed with the ALPHA= option.

DISTRIBUTION=keyword DIST=keyword

specifies the probability distribution for a mixture component.

If you specify the DIST= option and you do not specify a link function with the LINK= option, a default link function is chosen according to Table 39.5. If you do not specify a distribution, the FMM procedure defaults to the normal distribution for continuous response variables and to the binary distribution for classification or character variables, unless the events/trial syntax is used in the MODEL statement. If you choose the events/trial syntax, the FMM procedure defaults to the binomial distribution.

Table 39.5 lists keywords that you can specify for the DISTRIBUTION= option and the corresponding default link functions. For generalized linear models with these distributions, you can find expressions for the log-likelihood functions in the section Log-Likelihood Functions for Response Distributions.

Table 39.5: Keyword Values of the DIST= Option

			Default Link
keyword	Alias	Distribution	Function
BETA		Beta	Logit
BETABINOMIAL	BETABIN	Beta-binomial	Logit
BINARY	BERNOULLI	Binary	Logit
BINOMIAL	BIN	Binomial	Logit
BINOMCLUSTER	BINOMCLUS	Binomial cluster	Logit
CONSTANT <(c)>	DEGENERATE <(c)>	Degenerate	N/A
EXPONENTIAL	EXPO	Exponential	Log
FOLDEDNORMAL	FNORMAL	Folded normal	Identity
GAMMA	GAM	Gamma	Log
GAUSSIAN	NORMAL	Normal	Identity
GENPOISSON	GPOISSON	Generalized Poisson	Log
GEOMETRIC	GEOM	Geometric	Log
INVGAUSS	IGAUSSIAN, IG	Inverse Gaussian	Inverse squared
			(power(–2))
LOGNORMAL	LOGN	Lognormal	Identity
NEGBINOMIAL	NEGBIN, NB	Negative binomial	Log
POISSON	POI	Poisson	Log
T <( $\nu$ )>	STUDENT <( $\nu$ )>	t	Identity
TRUNCEXPO <(a,b)>	TEXPO <(a,b)>	Truncated exponential	Log
TRUNCLOGN <(a,b)>	TLOGN <(a,b)>	Lognormal	Identity
TRUNCNEGBIN	TNEGBIN, TNB	Negative binomial	Log
TRUNCNORMAL <(a,b)>	TNORMAL <(a,b)>	Truncated normal	Identity
TRUNCPOISSON	TPOISSON, TPOI	Truncated Poisson	Log
UNIFORM <(a,b)>	UNIF <(a,b)>	Uniform	N/A
WEIBULL		Weibull	Log

Note that the PROC FMM default link for the gamma or exponential distribution is not the canonical link (the reciprocal link).

The binomial cluster model is a two-component model described in Morel and Nagaraj (1993); Morel and Neerchal (1997); Neerchal and Morel (1998). See Example 39.1 for an application of the binomial cluster model in a teratological experiment.

If the events/trials syntax is used, the default distribution is the binomial and only the following choices are available: DIST=BINOMIAL, DIST=BETABINOMIAL, and DIST=BINOMCLUSTER. The trials variable is ignored for all other distributions. This enables you to fit models in which some components have a binomial or binomial-like distribution. For example, suppose that variable n is a binomial denominator and variable logn is its logarithm. Then the following statements model a two-component mixture of a binomial and Poisson count model:

model y/n  = ;
model      +  / dist=Poisson offset=logn;

The OFFSET= option is used in the second MODEL statement to specify that the Poisson counts refer to different base counts, because the trial variable n is ignored in the second model.

If DIST=BINOMIAL is specified without the events/trials syntax, then n=1 is used for the default number of trials.

DIST=TRUNCNEGBIN and DIST=TRUNCPOISSON are zero-truncated versions of DIST=NEGBINOMIAL and DIST=POISSON, respectively—that is, only the value of 0 is excluded from the support.

For DIST=TRUNCEXPO, DIST=TRUNCLOGN, and DIST=TRUNCNORMAL, you must specify the lower (a) and upper (b) truncation points of the distribution. For example:

DIST=TRUNCEXPO<(a,b)>
DIST=TRUNCLOGN<(a,b)>
DIST=TRUNCNORMAL<(a,b)>

Each of these distributions is the conditional version of its corresponding nontruncated distribution that is confined to the support $[a, b]$ (inclusive). You can specify a missing value (.) for either a or b to truncate only on the other side; that is, a=. indicates a right-truncated distribution, and b=. indicates a left-truncated distribution.

For several distribution specifications you can provide additional optional parameters to further define the distribution. These optional parameters are listed in the following:

CONSTANT<(c)>: The number c specifies the value where the mass is concentrated. The default is DIST=CONSTANT(0), so you can add zero-inflation to any model by adding a MODEL statement with DIST=CONSTANT.
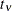T<( $\nu$ )>: The number $\nu$ specifies the degrees of freedom for the (shifted) t distribution. The default is DIST=T(3); this leads to a heavy-tailed distribution for which the variance is defined. See the section Log-Likelihood Functions for Response Distributions for the density function of the shifted $t_\nu$ distribution.
UNIFORM<(a,b)>: The values a and b define the support of the uniform distribution, a < b. By default, a = 0 and b = 1.

EQUATE=MEAN | SCALE | NONE | EFFECTS(effect-list)

specifies simple sets of parameter constraints across the components in a MODEL statement; the default is EQUATE=NONE. This option is available only for maximum likelihood estimation. If you specify EQUATE=MEAN, the parameters that determine the mean are reduced to a single set that is applicable to all components in the MODEL statement. If you specify EQUATE=SCALE, a single parameter represents the common scale for all components in the MODEL statement. The EFFECTS option enables you to force the parameters for the chosen model effects to be equal across components; however, the number of parameters is unaffected.

For example, the following statements fit a two-component multiple regression model in which the coefficients for variable logd vary by component and the intercepts and coefficients for variable dose are the same for the two components:

proc fmm;
   model num = dose logd / equate=effects(int dose) k=2;
run;

To fix all coefficients across the two components, you can write the MODEL statement as

model num = dose logd / equate=effects(int dose logd) k=2;

model num = dose logd / equate=mean k=2;

If you restrict all parameters in a k-component MODEL statement to be equal, the FMM procedure reduces the model to k=1.

K=n NUMBER=n

specifies the number of components the MODEL statement contributes to the overall mixture. For the binomial cluster model, this option is not available, because this model is a two-component model by definition.

KMAX=n

specifies the maximum number of components the MODEL statement contributes to the overall mixture.

If the maximum number of components in the mixture, as determined by all KMAX= options, is larger than the minimum number of components, the FMM procedure fits all possible models and displays summary fit information for the sequence of evaluated models. The “best” model according to the CRITERION= option in the PROC FMM statement is then chosen, and the remaining output and analyses performed by PROC FMM pertain to this “best” model.

When you use MCMC methods to estimate the parameters of a mixture, you need to ensure that the chain for a given value of k has converged; otherwise, comparisons among models that have varying numbers of components might not be meaningful. You can use the FITDETAILS option to display summary and diagnostic information for the MCMC chains from each model.

If you specify the KMIN= option but not the KMAX= option, then the default value for the KMAX= option is the value of the KMIN= option (unless KMIN=0, in which case the KMAX= option is set to 1).

KMIN=n

specifies the minimum number of components that the MODEL statement contributes to the overall mixture. When you use MCMC methods to estimate the parameters of a mixture, you need to ensure that the chain for a given value of k has converged; otherwise, comparisons among models that have varying numbers of components might not be meaningful.

KRESTART

requests that the starting values for each analysis (that is, for each unique number of components as determined by the KMIN= and KMAX= options) be determined separately, in the same way as if no other analyses were performed. If you do not specify the KRESTART option, then the starting values for each analysis are based on results from the previous analysis with one less component.

LABEL=’label’

specifies an optional label for the model that is used to identify the model in printed output, on graphics, and in data sets created from ODS tables.

LINK=keyword

specifies the link function in the model. The keywords and expressions for the associated link functions are shown in Table 39.6.

Table 39.6: Link Functions in MODEL Statement of the FMM Procedure

		Link
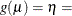
LINK=	Alias	Function	$g(\mu ) =\eta =$
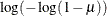
CLOGLOG	CLL	Complementary log-log	$\log (-\log (1-\mu ))$
IDENTITY	ID	Identity	$\mu$
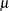
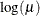
LOG		Log	$\log (\mu )$
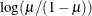
LOGIT		Logit	$\log (\mu /(1-\mu ))$
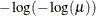
LOGLOG		Log-log	$-\log (-\log (\mu ))$
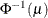
PROBIT	NORMIT	Probit	$\Phi ^{-1}(\mu )$
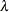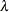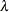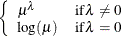
POWER( $\lambda$ )	POW( $\lambda$ )	Power with exponent $\lambda$ = number	$\left\{ \begin{array}{ll} \mu ^{\lambda } & \mr {if } \, \lambda \not= 0 \\ \log (\mu ) & \mr {if } \, \lambda = 0 \end{array} \right.$
POWERMINUS2		Power with exponent –2	$1/\mu ^2$
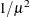
RECIPROCAL	INVERSE	Reciprocal	$1/\mu$

The default link functions for the various distributions are shown in Table 39.5.

NOINT

requests that no intercept be included in the model. An intercept is included by default, unless the distribution is DIST=CONSTANT or DIST=UNIFORM.

OFFSET=variable

specifies the offset variable function for the linear predictor in the model. An offset variable can be thought of as a regressor variable whose regression coefficient is known to be 1. For example, you can use an offset in a Poisson model when counts have been obtained in time intervals of different lengths. With a log link function, you can model the counts as Poisson variables with the logarithm of the time interval as the offset variable.

PARAMETERS(parameter-specification) PARMS(parameter-specification)

specifies starting values for the model parameters. If no PARMS option is specified, the FMM procedure determines starting values by using a data-dependent algorithm. To determine initial values for the Markov chain in Bayesian estimation, see the INITIAL= option in the BAYES statement. The specification of the parameters takes the following form: parameters in the mean function precede the scale parameters, and parameters for different components are separated by commas.

The following statements specify starting parameters for a two-component normal model. The initial values for the intercepts are 1 and –3; the initial values for the variances are 0.5 and 4.

proc fmm;
   model y = / k=2 parms(1 0.5, -3 4);
run;

You can specify missing values for parameters whose starting values are to be determined by the default method. Only values for parameters that participate in the optimization are specified. The values for model effects are specified on the linear (linked) scale.