Polynomial Effects :: SAS/STAT(R) 13.1 User's Guide

Polynomial Effects

EFFECT name=POLYNOMIAL (var-list </ polynomial-options>) ;

EFFECT name=POLY (var-list </ polynomial-options>) ;

The variables in var-list must be numeric. A design matrix column is generated for each term of the specified polynomial. By default, each of these terms is treated as a separate effect for the purpose of model building. For example, the statements

proc glmselect;
   effect MyPoly = polynomial(x1-x3/degree=2);
   model y = MyPoly;
run;

yield the identical analysis to the statements

proc glmselect;
   model y = x1 x2 x3 x1*x1 x1*x2 x1*x3 x2*x2 x2*x3 x3*x3;
run;

You can specify the following polynomial-options after a slash (/):

DEGREE=n

specifies the degree of the polynomial. The degree must be a positive integer. The degree is typically a small integer, such as 1, 2, or 3. The default is DEGREE=1.

DETAILS

requests a table that shows the details of the specified polynomial, including the number of terms generated. If you also specify the STANDARDIZE option, then a table that shows the standardization details is also produced.

LABELSTYLE=(style-opts) LABELSTYLE=style-opt

specifies how the terms in the polynomial are labeled. By default, powers are shown with ^ as the exponentiation operator and * as the multiplication operator. For example, a polynomial term such as 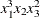$x_1^3 x_2 x_3^2$ is labeled x1^3*x2*x3^2. You can change the style of the label by using the following style-opts within parentheses. If you specify a single style-opt, then you can omit the enclosing parentheses.

EXPAND

specifies that each variable with an exponent greater than 1 be written as products of that variable. For example, the term 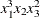$x_1^3 x_2 x_3^2$ receives the label x1*x1*x1*x2*x3*x3.

EXPONENT <=quoted string>

specifies that each variable with an exponent greater than 1 be written using exponential notation. By default, the symbol ^ is used as the exponentiation operator. If you supply the optional quoted string after an equal sign, then that string is used as the exponentiation operator. For example, if you specify

LABELSTYLE=(EXPONENT="**")

then the term 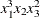$x_1^3 x_2 x_3^2$ receives the label x1**3*x2*x3**2.

INCLUDENAME

specifies that the name of the effect followed by an underscore be used as a prefix for term labels. For example, the following statement generates terms with labels MyPoly_x1 and MyPoly_x1^2:


EFFECT MyPoly=POLYNOMIAL(x1/degree=2 labelstyle=INCLUDENAME)

The INCLUDENAME option is ignored if you also specify the NOSEPARATE option in the EFFECT=POLYNOMIAL statement.

PRODUCTSYMBOL=NONE | quoted string

specifies that the supplied string be used as the product symbol. For example, the following statement generates terms with labels x1, x2, and x1 x2:


EFFECT MyPoly=POLYNOMIAL(x1 x2 / degree=2 mdegree=1
                                 labelstyle=(PRODUCTSYMBOL=" "))

If you specify PRODUCTSYMBOL=NONE, then the labels are formed by juxtaposing the constituent variable names.

MDEGREE=n

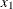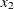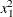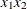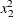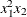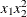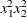specifies the maximum degree of any variable in a term of the polynomial. This degree must be a positive integer. The default is the degree of the specified polynomial. For example, the following statement generates the terms $x_1$ , $x_2$ , $x_1^2$ , $x_1 x_2$ , $x_2^2$ , $x_1^2 x_2$ , $x_1 x_2^2$ and $x_1^2 x_2^2$ :


EFFECT MyPoly=POLYNOMIAL(x1 x2/degree=4 MDEGREE=2);

NOSEPARATE

specifies that the polynomial be treated as a single effect with multiple degrees of freedom. The effect name that you specify is used as the constructed effect name, and the labels of the terms are used as labels of the corresponding parameters.

STANDARDIZE <(centerscale-opts)> <= standardize-opt>

specifies that the variables that define the polynomial be standardized. By default, the standardized variables receive prefix “s_” in the variable names.

You can use the following centerscale-opts to specify how the center and scale are estimated:

METHOD=MOMENTS: specifies that the center be estimated by the variable mean and the scale be estimated by the standard deviation. If a weight variable is specified using a WEIGHT statement, the observations with invalid weights are ignored when forming the mean and standard deviation, but the weights are otherwise not used. Only observations that are used in performing the analysis are used for the standardization.
METHOD=RANGE: specifies that the center be estimated by the midpoint of the variable range and the scale be estimated as half the variable range. Any observation that has a missing value for any regressor used in the model is ignored when computing the range of variables in a polynomial effect. Observations with valid regressor values but missing or invalid values of frequency variables, weight variables, or dependent variables are used in computing variable ranges. The default (if you do not specify the METHOD= suboption) is METHOD=RANGE.
METHOD=WMOMENTS: is the same as METHOD=MOMENTS except that weighted means and weighted standard deviations are used.

Let

$\begin{eqnarray*} n & = & \mr {number~ of~ observations~ used~ in~ the~ analysis} \\ w & = & \mr {weight~ variable} \\ f & = & \mr {frequency~ variable} \\ x & = & \mr {variable~ to~ be~ standardized} \\ x_{(n)}& = & \mbox{Max}_{i=1}^ n (x_ i) \\ x_{(1)}& = & \mbox{Min}_{i=1}^ n (x_ i) \\ F & = & \mr {sum~ of~ frequencies} \\ & = & \Sigma _{i=1}^ n f_ i \\ \mr {WF}& = & \mr {sum~ of~ weighted~ frequencies} \\ & = & \Sigma _{i=1}^ n w_ i f_ i \\ \end{eqnarray*}$

Table 19.12 shows how the center and scale are computed for each of the supported methods.

Table 19.12: Center and Scale Estimates by Method

Method	Center	Scale
Range	$(x_{(n)}+x_{(1)})/2$	$(x_{(n)}-x_{(1)})/2$
Moments	$\bar{x}=\Sigma _{i=1}^ n{f_ i x_ i} / F$	$\sqrt {\Sigma _{i=1}^ n {f_ i(x_ i-\bar{x})^2} / (F-1)}$
WMoments	$\bar{x}_ w=\Sigma _{i=1}^ n{w_ i f_ i x_ i} / \mr {WF}$	$\sqrt {\Sigma _{i=1}^ n {w_ i f_ i(x_ i-\bar{x}_ w)^2} / (F-1)}$

PREFIX=NONE | quoted-string: specifies the prefix that is appended to standardized variables when forming the term labels. If you omit this option, the default prefix is “s_”. If you specify PREFIX=NONE, then standardized variables are not prefixed.

You can control whether the standardization is to center, scale, or both center and scale by specifying a standardize-opt:

CENTER: specifies that variables be centered but not scaled. For a variable x,

$\mbox{s}\_ \text {x} = x - \mbox{center}$
CENTERSCALE: specifies that variables be centered and scaled. This is the default if you do not specify a standardization-opt. For a variable x,

$\mbox{s}\_ \text {x} = \frac{x - \mbox{center}}{\mbox{scale}}$
NONE: specifies that no standardization be performed.
SCALE: specifies that variables be scaled but not centered. For a variable x,

$\mbox{s}\_ \text {x} = \frac{x}{\mbox{scale}}$