Examples :: SAS/STAT(R) 13.1 User's Guide

A One-Way Classification Model

For the model

$Y = \mu + A_ i + \epsilon \quad \quad i = 1, 2, 3$

the general form of estimable functions $\mb {L}\bbeta$ is (from the previous example)

$\mb {L} \bbeta = \mathit{L1} \times \mu + \mathit{L2} \times A_1 + \mathit{L3} \times A_2 + (\mathit{L1}-\mathit{L2}-\mathit{L3}) \times A_3 ~$

Thus,

$\mb {L} = (\mathit{L1}, \mathit{L2}, \mathit{L3}, \mathit{L1}-\mathit{L2}-\mathit{L3})$

Tests involving only the parameters $A_1$ , $A_2$ , and $A_3$ must have an $\mb {L}$ of the form

$\mb {L} = (0, \mathit{L2}, \mathit{L3}, -\mathit{L2}-\mathit{L3}) ~$

Since this $\mb {L}$ for the A parameters involves only two symbols, hypotheses with at most two degrees of freedom can be constructed. For example, letting $(L2,L3)$ be $(1,0)$ and $(0,1)$ , respectively, yields

$\mb {L} = \left[ \begin{array}{rrrr} 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & -1 \end{array} \right]$

The preceding $\mb {L}$ can be used to test the hypothesis that $A_1=A_2=A_3$ . For this example, any $\mb {L}$ with two linearly independent rows with column 1 equal to zero produces the same sum of squares. For example, a joint test for linear and quadratic effects of A

$\mb {L} = \left[ \begin{array}{rrrr} 0 & 1 & 0 & -1 \\ 0 & 1 & -2 & 1 \end{array} \right]$

gives the same SS. In fact, for any $\mb {L}$ of full row rank and any nonsingular matrix $\mb {K}$ of conformable dimensions,

$\mbox{SS}(H_0\colon ~ \mb {L} \bbeta = 0) = \mbox{SS}(H_0\colon ~ \mb {KL} \bbeta = 0) ~$

A Three-Factor Main-Effects Model

Consider a three-factor main-effects model involving the CLASS variables A, B, and C, as shown in Table 15.1.

Table 15.1: Three-Factor Main-Effects Model

Obs	A	B	C
1	1	2	1
2	1	1	2
3	2	1	3
4	2	2	2
5	2	2	2

The general form of an estimable function is shown in Table 15.2.

Table 15.2: General Form of an Estimable Function for Three-Factor Main-Effects Model

Parameter		Coefficient
$\mu$ (Intercept)		L1
A1		L2
A2		L1 – L2
B1		L4
B2		L1 – L4
C1		L6
C2		L1 + L2 – L4 – 2 $\times$ L6
C3		–L2 + L4 + L6

Since only four symbols (L1, L2, L4, and L6) are involved, any testable hypothesis will have at most four degrees of freedom. If you form an $\mb {L}$ matrix with four linearly independent rows according to the preceding rules, then testing $\mb {L}\bbeta =\mb {0}$ is equivalent to testing that $\mr {E}[\mb {Y}]$ is uniformly 0. Symbolically,

$\mbox{SS}(H_0\colon ~ \mb {L} \bbeta = 0) = R(\mu , A, B, C) ~$

In a main-effects model, the usual hypothesis of interest for a main effect is the equality of all the parameters. In this example, it is not possible to unambiguously test such a hypothesis because of confounding: any test for the equality of the parameters for any one of A, B, or C will necessarily involve the parameters for the other two effects. One way to proceed is to construct a maximum rank hypothesis (MRH) involving only the parameters of the main effect in question. This can be done using the general form of estimable functions. Note the following:

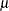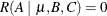To get an MRH involving only the parameters of A, the coefficients of $\mb {L}$ associated with $\mu$ , B1, B2, C1, C2, and C3 must be equated to zero. Starting at the top of the general form, let L1 = 0, then L4 = 0, then L6 = 0. If C2 and C3 are not to be involved, then L2 must also be zero. Thus, A1 – A2 is not estimable; that is, the MRH involving only the A parameters has zero rank and $R(A~ |~ \mu ,B,C)=0$ .
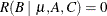To obtain the MRH involving only the B parameters, let L1 = L2 = L6 = 0. But then to remove C2 and C3 from the comparison, L4 must also be set to 0. Thus, B1 – B2 is not estimable and $R(B~ |~ \mu ,A,C)=0$ .
To obtain the MRH involving only the C parameters, let L1 = L2 = L4 =0. Thus, the MRH involving only C parameters is

$\mathit{C1} - 2 \times \mathit{C2} +\mathit{C3} = K \quad \quad \mbox{(for any } K\text {)}$

or any multiple of the left-hand side equal to K. Furthermore,

$\mbox{SS}(H_0\colon ~ \mathit{C1} - 2 \times \mathit{C2} + \mathit{C3} = 0) = R(C~ |~ \mu , A, B)$

A Multiple Regression Model

Suppose

$\mr {E}[Y] = \beta _0 + \beta _1 x_1 + \beta _2 x_2 + \beta _3 x_3$

where the $\mb {X’X}$ matrix has full rank. The general form of estimable functions is as shown in Table 15.3.

Table 15.3: General Form of Estimable Functions for a Multiple Regression Model When $\mb {X’X}$ Matrix Is of Full Rank

Parameter		Coefficient
$\beta _0$		L1
$\beta _1$		L2
$\beta _2$		L3
$\beta _3$		L4

For example, to test the hypothesis that $\beta _2=0$ , let L1 = L2 = L4 = 0 and let L3 = 1. Then SS $(\mb {L}\bbeta =\mb {0}) = R(\beta _2~ |~ \beta _0,\beta _1,\beta _3)$ . In this full-rank case, all parameters, as well as any linear combination of parameters, are estimable.

Suppose, however, that $X3=2 x_1 + 3 x_2$ . The general form of estimable functions is shown in Table 15.4.

Table 15.4: General Form of Estimable Functions for a Multiple Regression Model When $\mb {X’X}$ Matrix Is Not of Full Rank

Parameter		Coefficient
$\beta _0$		L1
$\beta _1$		L2
$\beta _2$		L3
$\beta _3$		$2 \times \mathit{L2}+3 \times \mathit{L3}$

For this example, it is possible to test $H_0\colon \beta _0 = 0$ . However, $\beta _1$ , $\beta _2$ , and $\beta _3$ are not jointly estimable; that is,

$\begin{eqnarray*} R(\beta _1~ |~ \beta _0, \beta _2, \beta _3) & = & 0 \\[0.05in] R(\beta _2~ |~ \beta _0, \beta _1, \beta _3) & = & 0 \\[0.05in] R(\beta _3~ |~ \beta _0, \beta _1, \beta _2) & = & 0 ~ \end{eqnarray*}$