The SURVEYMEANS Procedure

Ratio

When you use a RATIO statement, the procedure produces statistics requested by the statistic-keywords in the PROC SURVEYMEANS statement.

Suppose that you want to calculate the ratio of variable Y to variable X. Let $x_{hij}$ be the value of variable X for the jth member in cluster i in the hth stratum.

The ratio of Y to X is

$\widehat{R} = \frac{ \sum _{h=1}^ H\sum _{i=1}^{n_ h} \sum _{j=1}^{m_{hi}} ~ w_{hij} ~ y_{hij} }{ \sum _{h=1}^ H\sum _{i=1}^{n_ h} \sum _{j=1}^{m_{hi}} ~ w_{hij} ~ x_{hij} }$

PROC SURVEYMEANS uses the Taylor series method to estimate the variance of the ratio $\widehat{R}$ as

$\widehat{V}(\widehat{R}) = \sum _{h=1}^ H \widehat{V_ h}(\widehat{R})$

where, if $n_ h>1$ , then

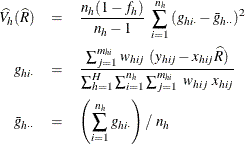
$\begin{eqnarray*} \widehat{V_ h}(\widehat{R}) & =& \frac{n_ h(1-f_ h)}{n_ h-1} ~ \sum _{i=1}^{n_ h} {(g_{hi\cdot }-\bar{g}_{h\cdot \cdot })^2}\\ g_{hi\cdot }& =& \frac{\sum _{j=1}^{m_{hi}}w_{hij}~ (y_{hij}- x_{hij}\widehat{R}) }{\sum _{h=1}^ H\sum _{i=1}^{n_ h} \sum _{j=1}^{m_{hi}} ~ w_{hij} ~ x_{hij}}\\ \bar{g}_{h\cdot \cdot } & =& \left( \sum _{i=1}^{n_ h}g_{hi\cdot } \right) / ~ n_ h \end{eqnarray*}$

and if $n_ h=1$ , then

$\widehat{V_ h}(\widehat{R}) = \left\{ \begin{array}{ll} \mbox{missing} & \mbox{ if } n_{h}=1 \mbox{ for } h’=1, 2, \ldots , H \\ 0 & \mbox{ if } n_{h}>1 \mbox{ for some } 1 \le h’ \le H \end{array} \right.$

The standard error of the ratio is the square root of the estimated variance:

$\mbox{StdErr}(\widehat{R})= \sqrt {\widehat{V}(\widehat{R})}$

When the denominator for a ratio is zero, then the value of the ratio is displayed as '–Infty', 'Infty', or a missing value, depending on whether the numerator is negative, positive, or zero, respectively; and the corresponding internal value is the special missing value '.M', the special missing value '.I', or the usual missing value, respectively.