Shared Concepts and Topics
This section discusses the construction of spline effects through the EFFECT statement. You can also include spline effects in statistical models by other means. The TRANSREG procedure has dedicated facilities for including regression splines in your model and controlling the construction of the splines. For example, you can use the TRANSREG procedure to fit a spline function but restrict the function to be always increasing or decreasing (monotone). See the section Using Splines and Knots in Chapter 104: The TRANSREG Procedure, for more information about using splines with the TRANSREG procedure. The GAM and TPSPLINE procedures also can model the effects of regressor variables in terms of smooth functions that are generated from spline bases. For more information see Chapter 41: The GAM Procedure, and Chapter 103: The TPSPLINE Procedure.
A spline effect expands variables into spline bases whose form depends on the options that you specify. You can find details about regression splines and spline bases in the section Splines and Spline Bases. You request a spline effect with the syntax
The variables in var-list must be numeric. Design matrix columns are generated separately for each of these variables, and the set of columns is collectively referred to with the specified name. By default, the spline basis that is generated for each variable is a cubic B-spline basis with three equally spaced knots positioned between the minimum and maximum values of that variable. This yields by default seven design matrix columns for each of the variables in the SPLINE effect.
You can specify the following spline-options after a slash (/):
- BASIS=BSPLINE
-
specifies a B-spline basis for the spline expansion. For splines of degree d defined with n knots, this basis consists of n + d + 1 columns. In order to completely specify the B-spline basis, d left-side boundary knots and
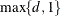 right-side boundary knots are also required. See the suboptions KNOTMETHOD=
, DATABOUNDARY
, KNOTMIN=
, and KNOTMAX=
for details about how to specify the positions of both the internal and boundary knots. This is the default if you do not
specify the BASIS= suboption.
right-side boundary knots are also required. See the suboptions KNOTMETHOD=
, DATABOUNDARY
, KNOTMIN=
, and KNOTMAX=
for details about how to specify the positions of both the internal and boundary knots. This is the default if you do not
specify the BASIS= suboption.
- BASIS=TPF(options)
-
specifies a truncated power function basis for the spline expansion. For splines of degree d defined with n knots for a variable x, this basis consists of an intercept, polynomials x,
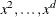 and one truncated power function for each of the n knots. Unlike the B-spline basis, no boundary knots are required. See the suboption KNOTMETHOD=
for details about how you can specify the position of the internal knots.
and one truncated power function for each of the n knots. Unlike the B-spline basis, no boundary knots are required. See the suboption KNOTMETHOD=
for details about how you can specify the position of the internal knots.
You can modify the number of columns when you request BASIS=TPF with the following options:
- DATABOUNDARY
-
specifies that the extremes of the data be used as boundary knots when building a B-spline basis.
- DEGREE=n
-
specifies the degree of the spline transformation. The degree must be a nonnegative integer. The degree is typically a small integer, such as 0, 1, 2, or 3. The default is DEGREE=3.
- DETAILS
-
requests tables that show the knot locations and the knots associated with each spline basis function.
- KNOTMAX=value
-
specifies that, for each variable in the EFFECT statement, the right-side boundary knots be equally spaced starting at the maximum of the variable and ending at the specified value. This option is ignored for variables whose maximum value is greater than the specified value or if the DATABOUNDARY option is also specified.
- KNOTMETHOD=knot-method<(knot-options)>
-
specifies how to construct the knots for spline effects. You can choose from the following knot-methods and affect the knot construction further with the method-specific knot-options:
- EQUAL<(n)>
-
specifies that n equally spaced knots be positioned between the extremes of the data. The default is n = 3. For a B-spline basis, any needed boundary knots continue to be equally spaced unless the DATABOUNDARY option has also been specified. KNOTMETHOD=EQUAL is the default if no knot-method is specified.
- LIST(number-list)
-
specifies the list of internal knots to be used in forming the spline basis columns. For a B-spline basis, the data extremes are used as boundary knots.
- LISTWITHBOUNDARY(number-list)
-
specifies the list of all knots that are used in forming the spline basis columns. When you use a truncated power function basis, this list is interpreted as the list of internal knots. When you use a B-spline basis of degree d, then the first d entries are used as left-side boundary knots and the last
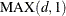 entries in the list are used as right-side boundary knots.
entries in the list are used as right-side boundary knots.
- MULTISCALE<(multiscale-options)>
-
specifies that multiple B-spline bases be generated, corresponding to sets with an increasing number of internal knots. As you increase the number of internal knots, the spline basis you generate is able to approximate features of the data at finer scales. So, by generating bases at multiple scales, you facilitate the modeling of both coarse- and fine-grained features of the data. For scale i, the spline basis corresponds to
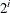 equally spaced internal knots. By default, the bases for scales 0–7 are generated. For each scale, a separate spline effect
is generated. The name of the constructed spline effect at scale i is formed by appending _Si to the effect name that you specify in the EFFECT statement. If you specify multiple variables in the EFFECT statement, then
spline bases are generated separately for each variable at each scale and the name of the corresponding effect is obtained
by appending the variable name followed by _Si to the name in the EFFECT statement. For example, the following statement generates effects named spl_x1_S0, spl_x1_S1, spl_x1_S2,
equally spaced internal knots. By default, the bases for scales 0–7 are generated. For each scale, a separate spline effect
is generated. The name of the constructed spline effect at scale i is formed by appending _Si to the effect name that you specify in the EFFECT statement. If you specify multiple variables in the EFFECT statement, then
spline bases are generated separately for each variable at each scale and the name of the corresponding effect is obtained
by appending the variable name followed by _Si to the name in the EFFECT statement. For example, the following statement generates effects named spl_x1_S0, spl_x1_S1, spl_x1_S2,
 , spl_x1_S7 and spl_x2_S1, spl_x2_S2,
, spl_x1_S7 and spl_x2_S1, spl_x2_S2,  , spl_x2_S7:
, spl_x2_S7:
EFFECT spl = spline(x1 x2 / knotmethod=multiscale);
The MULTISCALE option is ignored if you specify the BASIS=TPF spline-option. The MULTISCALE option is not available for spline effects that are specified in the RANDOM statement of the GLIMMIX procedure.
You can control which scales are included with the following multiscale-options:
- PERCENTILES(n)
-
requests that internal knots be placed at n equally spaced percentiles of the variable or variables named in the EFFECT statement. For example, the following statement positions internal knots at the deciles of the variable
x. For a B-spline basis, the extremes of the data are used as boundary knots:EFFECT spl = spline(x / knotmethod=percentiles(9));
- RANGEFRACTIONS(fraction-list)
-
requests that internal knots be placed at each fraction of the ranges of the variables in the EFFECT statement. For example, if variable
x1ranges between 1 and 3, and variablex2ranges between 0 and 20, then the following EFFECT statement uses internal knots 1.2, 2, and 2.5 for variable x1 and internal knots 2, 10, and 15 for variable x2:EFFECT spl = spline(x1 x2 / knotmethod=rangefractions(.1 .5 .75));
For a B-spline basis, the data extremes are used as boundary knots.
- KNOTMIN=value
-
specifies that for each variable in the EFFECT statement, the left-side boundary knots be equally spaced starting at the specified value and ending at the minimum of the variable. This option is ignored for variables whose minimum value is less than the specified value or if the DATABOUNDARY option is also specified.
- NATURALCUBIC
-
specifies a natural cubic spline basis for the spline expansion. Natural cubic splines, also known as restricted cubic splines, are cubic splines that are constrained to be linear beyond the extreme knots. The natural cubic spline basis that is produced by the EFFECT statement is obtained by starting from the unrestricted truncated power function cubic spline basis that is defined with n distinct knots and imposes the linearity constraints beyond the extreme knots. This basis consists of an intercept, the polynomial x, and n – 2 functions that are all linear beyond the largest knot. The ith function,
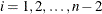 , is zero to the left of the ith knot, which is called the "break knot." See the section Splines and Spline Bases for details of this basis. You can use the NOINT and NOPOWERS suboptions of the BASIS=TPF option to suppress the intercept
and polynomial x when forming the columns of the natural cubic spline basis. When you specify the NATURALCUBIC option, the options BASIS=BSPLINE,
DATABOUNDARY, DEGREE=, and KNOTMETHOD=MULTISCALE are not applicable.
, is zero to the left of the ith knot, which is called the "break knot." See the section Splines and Spline Bases for details of this basis. You can use the NOINT and NOPOWERS suboptions of the BASIS=TPF option to suppress the intercept
and polynomial x when forming the columns of the natural cubic spline basis. When you specify the NATURALCUBIC option, the options BASIS=BSPLINE,
DATABOUNDARY, DEGREE=, and KNOTMETHOD=MULTISCALE are not applicable.
- SEPARATE
-
specifies that when multiple variables are specified in the EFFECT statement, the spline basis for each variable be treated as a separate effect. The names of these separated effects are formed by appending an underscore followed by the name of the variable to the name that you specify in the EFFECT statement. For example, the effect names generated with the following statement are spl_x1 and spl_x2:
EFFECT spl = spline(x1 x2 / separate);
In procedures that support variable selection, such as the GLMSELECT procedure, these two effects can enter or leave the model independently during the selection process. Separated effects are not supported in the RANDOM statement of the GLIMMIX procedure.
- SPLIT
-
specifies that each individual column in the design matrix that corresponds to the spline effect be treated as a separate effect that can enter or leave the model independently. Names for these split effects are generated by appending the variable name and an index for each column to the name that you specify in the EFFECT statement. For example, the effects generated for the spline effect in the following statement are spl_x1:1, spl_x1:2, …, spl_x1:7 and spl_x2:1, spl_x2:2, …, spl_x2:7:
EFFECT spl = spline(x1 x2 / split);
The SPLIT option is not supported in the GLIMMIX procedure.