Shared Concepts and Topics

References

  • Afifi, A. A. and Azen, S. P. (1972), Statistical Analysis: A Computer-Oriented Approach, New York: Academic Press.

  • Beale, E. M. L. (1972), “A Derivation of Conjugate Gradients,” in F. A. Lootsma, ed., Numerical Methods for Nonlinear Optimization, London: Academic Press.

  • Browne, M. W. (1982), “Covariance Structures,” in D. M. Hawkins, ed., Topics in Applied Multivariate Analysis, 72–141, Cambridge: Cambridge University Press.

  • Dennis, J. E., Gay, D. M., and Welsch, R. E. (1981), “An Adaptive Nonlinear Least-Squares Algorithm,” ACM Transactions on Mathematical Software, 7, 348–368.

  • Dennis, J. E. and Mei, H. H. W. (1979), “Two New Unconstrained Optimization Algorithms Which Use Function and Gradient Values,” Journal of Optimization Theory and Applications, 28, 453–482.

  • Dunnett, C. W. (1980), “Pairwise Multiple Comparisons in the Unequal Variance Case,” Journal of the American Statistical Association, 75, 796–800.

  • Edwards, D. and Berry, J. J. (1987), “The Efficiency of Simulation-Based Multiple Comparisons,” Biometrics, 43, 913–928.

  • Eskow, E. and Schnabel, R. B. (1991), “Algorithm 695: Software for a New Modified Cholesky Factorization,” ACM Transactions on Mathematical Software, 17, 306–312.

  • Fletcher, R. (1987), Practical Methods of Optimization, 2nd Edition, Chichester, UK: John Wiley & Sons.

  • Fox, J. (1987), “Effect Displays for Generalized Linear Models,” in C. C. Clogg, ed., Sociological Methodology, 347–361, Washington, DC: American Sociological Association.

  • Frankel, S. A. (1961), “Statistical Design of Experiments for Process Development of MBT,” Rubber Age, 89, 453.

  • Friendly, M. (2000), Visualizing Categorical Data, Cary, NC: SAS Institute Inc.

  • Games, P. A. and Howell, J. F. (1976), “Pairwise Multiple Comparison Procedures with Unequal n’s and/or Variances: A Monte Carlo Study,” Journal of Educational Statistics, 1, 113–125.

  • Gay, D. M. (1983), “Subroutines for Unconstrained Minimization,” ACM Transactions on Mathematical Software, 9, 503–524.

  • Guirguis, G. H. and Tobias, R. D. (2004), “On the Computation of the Distribution for the Analysis of Means,” Communications in Statistics—Simulation and Computation, 33, 861–888.

  • Hastie, T. J., Tibshirani, R. J., and Friedman, J. H. (2001), The Elements of Statistical Learning, New York: Springer-Verlag.

  • Holm, S. (1979), “A Simple Sequentially Rejective Multiple Test Procedure,” Scandinavian Journal of Statistics, 6, 65–70.

  • Hsu, J. C. (1992), “The Factor Analytic Approach to Simultaneous Inference in the General Linear Model,” Journal of Computational and Graphical Statistics, 1, 151–168.

  • Hsu, J. C. (1996), Multiple Comparisons: Theory and Methods, London: Chapman & Hall.

  • Hsu, J. C. and Peruggia, M. (1994), “Graphical Representation of Tukey’s Multiple Comparison Method,” Journal of Computational and Graphical Statistics, 3, 143–161.

  • Kenward, M. G. and Roger, J. H. (1997), “Small Sample Inference for Fixed Effects from Restricted Maximum Likelihood,” Biometrics, 53, 983–997.

  • Kramer, C. Y. (1956), “Extension of Multiple Range Tests to Group Means with Unequal Numbers of Replications,” Biometrics, 12, 307–310.

  • Kutner, M. H. (1974), “Hypothesis Testing in Linear Models (Eisenhart Model),” American Statistician, 28, 98–100.

  • Moré, J. J. (1978), “The Levenberg-Marquardt Algorithm: Implementation and Theory,” in G. A. Watson, ed., Lecture Notes in Mathematics, volume 30, 105–116, Berlin: Springer-Verlag.

  • Moré, J. J. and Sorensen, D. C. (1983), “Computing a Trust-Region Step,” SIAM Journal on Scientific and Statistical Computing, 4, 553–572.

  • Myers, R. H. (1976), Response Surface Methodology, Blacksburg: Virginia Polytechnic Institute and State University.

  • Nelson, P. R. (1982), “Exact Critical Points for the Analysis of Means,” Communications in Statistics—Theory and Methods, 11, 699–709.

  • Nelson, P. R. (1991), “Numerical Evaluation of Multivariate Normal Integrals with Correlations 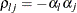$\rho _{lj} = -\alpha _ l\alpha _ j$,” in A. Öztürk and E. C. van der Meulen, eds., Frontiers of Statistical Scientific Theory and Industrial Applications: Proceedings of the ICOSCO I Conference, 97–114, Columbus, OH: American Sciences Press.

  • Nelson, P. R. (1993), “Additional Uses for the Analysis of Means and Extended Tables of Critical Values,” Technometrics, 35, 61–71.

  • Ott, E. R. (1967), “Analysis of Means: A Graphical Procedure,” Industrial Quality Control, 24, 101–109, reprinted in Journal of Quality Technology, 15 (1983), 10–18.

  • Polak, E. (1971), Computational Methods in Optimization, New York: Academic Press.

  • Powell, M. J. D. (1977), “Restart Procedures for the Conjugate Gradient Method,” Mathematical Programming, 12, 241–254.

  • Powell, M. J. D. (1978a), “Algorithms for Nonlinear Constraints That Use Lagrangian Functions,” Mathematical Programming, 14, 224–248.

  • Powell, M. J. D. (1978b), “A Fast Algorithm for Nonlinearly Constrained Optimization Calculations,” in G. A. Watson, ed., Lecture Notes in Mathematics, volume 630, 144–175, Berlin: Springer-Verlag.

  • Powell, M. J. D. (1982a), “Extensions to Subroutine VF02AD,” in R. F. Drenick and F. Kozin, eds., Systems Modeling and Optimization, Lecture Notes in Control and Information Sciences, volume 38, 529–538, Berlin: Springer-Verlag.

  • Powell, M. J. D. (1982b), VMCWD: A Fortran Subroutine for Constrained Optimization, Technical Report DAMTP 1982/NA4, Cambridge University.

  • Royen, T. (1989), “Generalized Maximum Range Tests for Pairwise Comparisons of Several Populations,” Biometrical Journal, 31, 905–929.

  • Shaffer, J. P. (1986), “Modified Sequentially Rejective Multiple Test Procedures,” Journal of the American Statistical Association, 81, 826–831.

  • Silvapulle, M. J. and Sen, P. K. (2004), Constrained Statistical Inference: Order, Inequality, and Shape Constraints, New York: John Wiley & Sons.

  • Tamhane, A. C. (1979), “A Comparison of Procedures for Multiple Comparisons of Means with Unequal Variances,” Journal of the American Statistical Association, 74, 471–480.

  • Westfall, P. H. (1997), “Multiple Testing of General Contrasts Using Logical Constraints and Correlations,” Journal of the American Statistical Association, 92, 299–306.

  • Westfall, P. H., Tobias, R. D., Rom, D., Wolfinger, R. D., and Hochberg, Y. (1999), Multiple Comparisons and Multiple Tests Using the SAS System, Cary, NC: SAS Institute Inc.

  • Westfall, P. H. and Young, S. S. (1993), Resampling-Based Multiple Testing: Examples and Methods for p-Value Adjustment, New York: John Wiley & Sons.

  • Winer, B. J. (1971), Statistical Principles in Experimental Design, 2nd Edition, New York: McGraw-Hill.