Introduction to Statistical Modeling with SAS/STAT Software
The least squares principle does not provide for a parameter estimator for ![]() . The usual approach is to use a method-of-moments estimator that is based on the sum of squared residuals. If the model is
correct, then the mean square for error, defined to be
. The usual approach is to use a method-of-moments estimator that is based on the sum of squared residuals. If the model is
correct, then the mean square for error, defined to be ![]() divided by its degrees of freedom,
divided by its degrees of freedom,
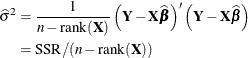
is an unbiased estimator of ![]() .
.