Introduction to Regression Procedures
-
Allen, D. M. (1971), “Mean Square Error of Prediction as a Criterion for Selecting Variables,” Technometrics, 13, 469–475.
-
Allen, D. M. and Cady, F. B. (1982), Analyzing Experimental Data by Regression, Belmont, CA: Lifetime Learning Publications.
-
Belsley, D. A., Kuh, E., and Welsch, R. E. (1980), Regression Diagnostics: Identifying Influential Data and Sources of Collinearity, New York: John Wiley & Sons.
-
Bock, R. D. (1975), Multivariate Statistical Methods in Behavioral Research, New York: McGraw-Hill.
-
Box, G. E. P. (1966), “The Use and Abuse of Regression,” Technometrics, 8, 625–629.
-
Box, G. E. P. and Cox, D. R. (1964), “An Analysis of Transformations,” Journal of the Royal Statistical Society, Series B, 26, 211–234.
-
Cleveland, W. S., Devlin, S. J., and Grosse, E. (1988), “Regression by Local Fitting,” Journal of Econometrics, 37, 87–114.
-
Cook, R. D. (1977), “Detection of Influential Observations in Linear Regression,” Technometrics, 19, 15–18.
-
Cook, R. D. (1979), “Influential Observations in Linear Regression,” Journal of the American Statistical Association, 74, 169–174.
-
Daniel, C. and Wood, F. S. (1999), Fitting Equations to Data: Computer Analysis of Multifactor Data, 2nd Edition, New York: John Wiley & Sons.
-
Darlington, R. B. (1968), “Multiple Regression in Psychological Research and Practice,” Psychological Bulletin, 69, 161–182.
-
Davis, A. W. (1970), “Differential Equation of Hotelling’s Generalized
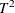 ,” Annals of Statistics, 39, 815–832.
,” Annals of Statistics, 39, 815–832.
-
Davis, A. W. (1972), “On the Marginal Distributions of the Latent Roots of the Multivariate Beta Matrix,” Biometrika, 43, 1664–1670.
-
Davis, A. W. (1979), “On the Differential Equation for Meijer’s
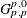 Function, and Further Tables of Wilks’s Likelihood Ratio Criterion,” Biometrika, 66, 519–531.
Function, and Further Tables of Wilks’s Likelihood Ratio Criterion,” Biometrika, 66, 519–531.
-
Davis, A. W. (1980), “Further Tabulation of Hotelling’s Generalized
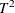 ,” Communications in Statistics—Simulation and Computation, 9, 321–336.
,” Communications in Statistics—Simulation and Computation, 9, 321–336.
-
Draper, N. R. and Smith, H. (1998), Applied Regression Analysis, 3rd Edition, New York: John Wiley & Sons.
-
Durbin, J. and Watson, G. S. (1951), “Testing for Serial Correlation in Least Squares Regression,” Biometrika, 37, 409–428.
-
Efron, B., Hastie, T. J., Johnstone, I. M., and Tibshirani, R. (2004), “Least Angle Regression (with Discussion),” Annals of Statistics, 32, 407–499.
-
Eilers, P. H. C. and Marx, B. D. (1996), “Flexible Smoothing with B-Splines and Penalties,” Statistical Science, 11, 89–121, with discussion.
-
Freund, R. J. and Littell, R. C. (1986), SAS System for Regression, 1986 Edition, Cary, NC: SAS Institute Inc.
-
Freund, R. J., Littell, R. C., and Spector, P. C. (1991), SAS System for Linear Models, Cary, NC: SAS Institute Inc.
-
Friedman, J. H. (1991), “Multivariate Adaptive Regression Splines,” Annals of Statistics, 19, 1–67.
-
Gentleman, W. M. (1972), Basic Procedures for Large, Sparse, or Weighted Least Squares Problems, Technical Report CSRR-2068, University of Waterloo, Ontario.
-
Gentleman, W. M. (1973), “Least Squares Computations by Givens Transformations without Square Roots,” Journal of the Institute of Mathematics and Its Applications, 12, 329–336.
-
Goodnight, J. H. (1979), “A Tutorial on the Sweep Operator,” American Statistician, 33, 149–158.
-
Hawkins, D. M. (1980), “A Note on Fitting a Regression with No Intercept Term,” American Statistician, 34, 233.
-
Hosmer, D. W., Jr. and Lemeshow, S. (1989), Applied Logistic Regression, New York: John Wiley & Sons.
-
Huber, P. J. (1973), “Robust Regression: Asymptotics, Conjectures, and Monte Carlo,” Annals of Statistics, 1, 799–821.
-
Johnston, J. and DiNardo, J. (1997), Econometric Methods, 4th Edition, New York: McGraw-Hill.
-
Kennedy, W. J., Jr. and Gentle, J. E. (1980), Statistical Computing, New York: Marcel Dekker.
-
Kvalseth, T. O. (1985), “Cautionary Note about
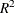 ,” American Statistician, 39, 279–285.
,” American Statistician, 39, 279–285.
-
Lee, Y. (1972), “Some Results on the Distribution of Wilks’ Likelihood Ratio Criterion,” Biometrika, 95, 649.
-
Mallows, C. L. (1973), “Some Comments on
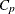 ,” Technometrics, 15, 661–675.
,” Technometrics, 15, 661–675.
-
Mardia, K. V., Kent, J. T., and Bibby, J. M. (1979), Multivariate Analysis, London: Academic Press.
-
Morrison, D. F. (2004), Multivariate Statistical Methods, 4th Edition, New York: Duxbury Press.
-
Mosteller, F. and Tukey, J. W. (1977), Data Analysis and Regression, Reading, MA: Addison-Wesley.
-
Muller, K. E. (1998), “A New F Approximation for the Pillai-Bartlett Trace under
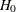 ,” Journal of Computational and Graphical Statistics, 7, 131–137.
,” Journal of Computational and Graphical Statistics, 7, 131–137.
-
Neter, J. and Wasserman, W. (1974), Applied Linear Statistical Models, Homewood, IL: Irwin.
-
Pillai, K. C. S. (1960), Statistical Table for Tests of Multivariate Hypotheses, Manila: Statistical Center, University of Philippines.
-
Pillai, K. C. S. and Flury, B. N. (1984), “Percentage Points of the Largest Characteristic Root of the Multivariate Beta Matrix,” Communications in Statistics—Theory and Methods, 13, 2199–2237.
-
Pindyck, R. S. and Rubinfeld, D. L. (1981), Econometric Models and Econometric Forecasts, 2nd Edition, New York: McGraw-Hill.
-
Rao, C. R. (1973), Linear Statistical Inference and Its Applications, 2nd Edition, New York: John Wiley & Sons.
-
Rawlings, J. O. (1988), Applied Regression Analysis: A Research Tool, Pacific Grove, CA: Wadsworth & Brooks/Cole Advanced Books & Software.
-
Rousseeuw, P. J. (1984), “Least Median of Squares Regression,” Journal of the American Statistical Association, 79, 871–880.
-
Rousseeuw, P. J. and Yohai, V. (1984), “Robust Regression by Means of S-Estimators,” in J. Franke, W. Härdle, and R. D. Martin, eds., Robust and Nonlinear Time Series Analysis, number 26 in Lecture Notes in Statistics, 256–274, Berlin: Springer-Verlag.
-
Tibshirani, R. (1996), “Regression Shrinkage and Selection via the Lasso,” Journal of the Royal Statistical Society, Series B, 58, 267–288.
-
Timm, N. H. (2002), Applied Multivariate Analysis, New York: Springer.
-
Weisberg, S. (1985), Applied Linear Regression, 2nd Edition, New York: John Wiley & Sons.
-
Weisberg, S. (2005), Applied Linear Regression, 3rd Edition, New York: John Wiley & Sons.
-
Yohai, V. J. (1987), “High Breakdown Point and High Efficiency Robust Estimates for Regression,” Annals of Statistics, 15, 642–656.
-
Younger, M. S. (1979), Handbook for Linear Regression, North Scituate, MA: Duxbury Press.