The SURVEYPHREG Procedure

Variance Adjustment Factors

PROC SURVEYPHREG provides options for adjustment of the default variance estimators. VADJUST=NONE and VADJUST=DF are available for the Taylor series linearization variance estimator. VADJUST=AVGREPSS is available for the jackknife replication variance estimators.

For models with large number of parameters, it is reasonable to adjust the Taylor series linearized variance estimator by the number of estimable parameters in the analysis model. Fuller et al. (1989, pp. 77–81) use an adjustment factor $(n-1)/(n-p)$ to estimate the linearized variance for regression coefficients, where n is the total number of observation units and p is the number of estimable parameters in the analysis model. By default, PROC SURVEYPHREG uses this adjustment in the computation of the matrix $\mb{G}$ for the Taylor series linearization variance estimation . If you do not want to use this adjustment, then specify VADJUST=NONE.

Variance adjustment factors can be useful for replication variance estimations, especially if some replicate samples are not usable. A replicate sample might not provide useful parameter estimates (replicate estimates) for reasons such as nonconvergence of the optimization or inestimability of some parameters in that subsample. For example, consider the jackknife variance estimator with R replicates. Suppose that only $R_ a (<R)$ replicates are used to obtain replicate estimates and $R-R_ a$ replicates cannot be used due to, say, nonconvergence of the optimization. Without loss of generality, assume that the first $R_ a$ replicates are used. By default SURVEYPHREG uses

\[ \widehat{\mb{V}}(\hat{\bbeta }) = \sum _{r=1}^{R_ a} \alpha _ r \left( {\hat{\bbeta }_ r} - \hat{\bbeta } \right) \left( {\hat{\bbeta }_ r} - \hat{\bbeta } \right)’ \]

as the jackknife variance estimator. An alternative estimator is

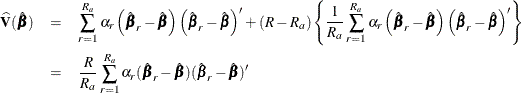
\begin{eqnarray*} \widehat{\mb{V}}(\hat{\bbeta }) & = & \sum _{r=1}^{R_ a} \alpha _ r \left( {\hat{\bbeta }_ r} - \hat{\bbeta } \right) \left( {\hat{\bbeta }_ r} - \hat{\bbeta } \right)’ + (R-R_ a) \left\{ \frac{1}{R_ a} \sum _{r=1}^{R_ a} \alpha _ r \left( {\hat{\bbeta }_ r} - \hat{\bbeta } \right) \left( {\hat{\bbeta }_ r} - \hat{\bbeta } \right)’ \right\} \\ & = & \frac{R}{R_ a} \sum _{r=1}^{R_ a} \alpha _ r(\hat{\bbeta }_ r - \hat{\bbeta }) (\hat{\bbeta }_ r - \hat{\bbeta })’ \end{eqnarray*}

which uses the average replicate sum of squares for the $R-R_ a$ unusable replicate samples. If you specify the VADJUST=AVGREPSS option, PROC SURVEYPHREG uses the second variance estimator for the jackknife replication method. Note that you can specify the FAY method-option for the BRR method to avoid nonconvergence of the optimization or inestimability of some parameters in subsamples.