The SURVEYPHREG Procedure
- Overview
- Getting Started
-
Syntax
 PROC SURVEYPHREG StatementBY StatementCLASS StatementCLUSTER StatementDOMAIN StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementProgramming StatementsREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementWEIGHT Statement
PROC SURVEYPHREG StatementBY StatementCLASS StatementCLUSTER StatementDOMAIN StatementESTIMATE StatementFREQ StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementNLOPTIONS StatementOUTPUT StatementProgramming StatementsREPWEIGHTS StatementSLICE StatementSTORE StatementSTRATA StatementTEST StatementWEIGHT Statement -
Details
 Notation and EstimationFailure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelSpecifying the Sample DesignMissing ValuesVariance EstimationDomain AnalysisHypothesis Tests, Confidence Intervals, and ResidualsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics
Notation and EstimationFailure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelSpecifying the Sample DesignMissing ValuesVariance EstimationDomain AnalysisHypothesis Tests, Confidence Intervals, and ResidualsOutput Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
For a testable hypothesis ![]() , the Wald F statistic is computed as
, the Wald F statistic is computed as
where ![]() is a contrast vector or matrix that you specify,
is a contrast vector or matrix that you specify, ![]() is the vector of regression parameters,
is the vector of regression parameters, ![]() is the estimated regression coefficients,
is the estimated regression coefficients, ![]() is the estimated covariance matrix of
is the estimated covariance matrix of ![]() , rank(
, rank(![]() ) is the rank of
) is the rank of ![]() , and
, and ![]() is a matrix such that
is a matrix such that
-
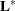 has the same number of columns as
has the same number of columns as 
-
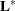 has full row rank
has full row rank
-
the rank of
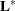 equals the rank of the
equals the rank of the  matrix
matrix
-
all rows of
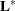 are estimable functions
are estimable functions
-
the Wald F statistic computed by using the
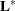 matrix is equivalent to the Wald F statistic computed by using the
matrix is equivalent to the Wald F statistic computed by using the  matrix with any row deleted that is a linear combination of previous rows
matrix with any row deleted that is a linear combination of previous rows
If ![]() is a full-rank matrix and all rows of
is a full-rank matrix and all rows of ![]() are estimable functions, then
are estimable functions, then ![]() is the same as
is the same as ![]() . It is possible that
. It is possible that ![]() matrix cannot be constructed for a given set of linear contrasts, in which case the contrasts are not testable.
matrix cannot be constructed for a given set of linear contrasts, in which case the contrasts are not testable.
If the DF=NONE option in the MODEL statement is specified, then the procedure performs a chi-square significance test.