The COUNTREG Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Specification of RegressorsMissing ValuesPoisson RegressionNegative Binomial RegressionZero-Inflated Count Regression OverviewZero-Inflated Poisson RegressionZero-Inflated Negative Binomial RegressionVariable SelectionComputational ResourcesNonlinear Optimization OptionsCovariance Matrix TypesDisplayed OutputOUTPUT OUT= Data SetOUTEST= Data SetODS Table Names
Specification of RegressorsMissing ValuesPoisson RegressionNegative Binomial RegressionZero-Inflated Count Regression OverviewZero-Inflated Poisson RegressionZero-Inflated Negative Binomial RegressionVariable SelectionComputational ResourcesNonlinear Optimization OptionsCovariance Matrix TypesDisplayed OutputOUTPUT OUT= Data SetOUTEST= Data SetODS Table Names -
Examples

- References
Example 11.2 ZIP and ZINB Models for Data Exhibiting Extra Zeros
In the study by Long (1997) of the number of published articles by scientists (see the section Getting Started: COUNTREG Procedure), the observed proportion of scientists who publish no articles is 0.3005. The following statements use PROC FREQ to compute the proportion of scientists who publish each observed number of articles. Output 11.2.1 shows the results.
proc freq data=long97data;
table art / out=obs;
run;
Output 11.2.1: Proportion of Scientists Who Publish a Certain Number of Articles
| art | Frequency | Percent | Cumulative Frequency |
Cumulative Percent |
|---|---|---|---|---|
| 0 | 275 | 30.05 | 275 | 30.05 |
| 1 | 246 | 26.89 | 521 | 56.94 |
| 2 | 178 | 19.45 | 699 | 76.39 |
| 3 | 84 | 9.18 | 783 | 85.57 |
| 4 | 67 | 7.32 | 850 | 92.90 |
| 5 | 27 | 2.95 | 877 | 95.85 |
| 6 | 17 | 1.86 | 894 | 97.70 |
| 7 | 12 | 1.31 | 906 | 99.02 |
| 8 | 1 | 0.11 | 907 | 99.13 |
| 9 | 2 | 0.22 | 909 | 99.34 |
| 10 | 1 | 0.11 | 910 | 99.45 |
| 11 | 1 | 0.11 | 911 | 99.56 |
| 12 | 2 | 0.22 | 913 | 99.78 |
| 16 | 1 | 0.11 | 914 | 99.89 |
| 19 | 1 | 0.11 | 915 | 100.00 |
PROC COUNTREG is then used to fit Poisson and negative binomial models to the data. For each model, the PROBCOUNT option computes
the probability that the number of published articles is ![]() , for m = 0 to 10.The following statements compute the estimates for Poisson and negative binomial models. The MEAN procedure
is then used to compute the average probability of a zero response.
, for m = 0 to 10.The following statements compute the estimates for Poisson and negative binomial models. The MEAN procedure
is then used to compute the average probability of a zero response.
proc countreg data=long97data;
model art=fem mar kid5 phd ment / dist=poisson;
output out=predpoi probcount(0 to 10);
run;
proc means mean data=predpoi;
var p_0;
run;
The output from the Poisson model for the COUNTREG and MEAN procedures is shown in Output 11.2.2.
Output 11.2.2: Poisson Model Estimation
| Model Fit Summary | |
|---|---|
| Dependent Variable | art |
| Number of Observations | 915 |
| Data Set | WORK.LONG97DATA |
| Model | Poisson |
| Log Likelihood | -1651 |
| Maximum Absolute Gradient | 3.5741E-9 |
| Number of Iterations | 5 |
| Optimization Method | Newton-Raphson |
| AIC | 3314 |
| SBC | 3343 |
| Algorithm converged. |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | t Value | Approx Pr > |t| |
| Intercept | 1 | 0.304617 | 0.102982 | 2.96 | 0.0031 |
| fem | 1 | -0.224594 | 0.054614 | -4.11 | <.0001 |
| mar | 1 | 0.155243 | 0.061375 | 2.53 | 0.0114 |
| kid5 | 1 | -0.184883 | 0.040127 | -4.61 | <.0001 |
| phd | 1 | 0.012823 | 0.026397 | 0.49 | 0.6271 |
| ment | 1 | 0.025543 | 0.002006 | 12.73 | <.0001 |
| Analysis Variable : P_0 Probability of art taking level=0 |
|---|
| Mean |
| 0.2092071 |
The following statements show the syntax for the negative binomial model:
proc countreg data=long97data;
model art=fem mar kid5 phd ment / dist=negbin(p=2) method=qn;
output out=prednb probcount(0 to 10);
run;
proc means mean data=prednb;
var p_0;
run;
Output 11.2.3 shows the results of the preceding statements.
Output 11.2.3: Negative Binomial Model Estimation
| Model Fit Summary | |
|---|---|
| Dependent Variable | art |
| Number of Observations | 915 |
| Data Set | WORK.LONG97DATA |
| Model | NegBin |
| Log Likelihood | -1561 |
| Maximum Absolute Gradient | 1.75584E-6 |
| Number of Iterations | 16 |
| Optimization Method | Quasi-Newton |
| AIC | 3136 |
| SBC | 3170 |
| Algorithm converged. |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | t Value | Approx Pr > |t| |
| Intercept | 1 | 0.256144 | 0.138560 | 1.85 | 0.0645 |
| fem | 1 | -0.216418 | 0.072672 | -2.98 | 0.0029 |
| mar | 1 | 0.150489 | 0.082106 | 1.83 | 0.0668 |
| kid5 | 1 | -0.176415 | 0.053060 | -3.32 | 0.0009 |
| phd | 1 | 0.015271 | 0.036040 | 0.42 | 0.6718 |
| ment | 1 | 0.029082 | 0.003470 | 8.38 | <.0001 |
| _Alpha | 1 | 0.441620 | 0.052967 | 8.34 | <.0001 |
| Analysis Variable : P_0 Probability of art taking level=0 |
|---|
| Mean |
| 0.3035957 |
For each model, the predicted proportion of zero articles can be calculated as the average predicted probability of zero articles
across all scientists. Under the Poisson model, the predicted proportion of zero articles is 0.2092, which considerably underestimates
the observed proportion. The negative binomial more closely estimates the proportion of zeros (0.3036). Also, the test of
the dispersion parameter, _Alpha, in the negative binomial model indicates significant overdispersion (![]() ). As a result, the negative binomial model is preferred to the Poisson model.
). As a result, the negative binomial model is preferred to the Poisson model.
Another way to account for the large number of zeros in this data set is to fit a zero-inflated Poisson (ZIP) or a zero-inflated
negative binomial (ZINB) model. In the following statements, DIST=ZIP requests the ZIP model. In the ZEROMODEL statement,
you can specify the predictors, ![]() , for the process that generated the additional zeros. The ZEROMODEL statement also specifies the model for the probability
, for the process that generated the additional zeros. The ZEROMODEL statement also specifies the model for the probability
![]() . By default, a logistic model is used for
. By default, a logistic model is used for ![]() . The default can be changed using the LINK= option. In this particular ZIP model, all variables used to model the article
counts are also used to model
. The default can be changed using the LINK= option. In this particular ZIP model, all variables used to model the article
counts are also used to model ![]() .
.
proc countreg data=long97data;
model art = fem mar kid5 phd ment / dist=zip;
zeromodel art ~ fem mar kid5 phd ment;
output out=predzip probcount(0 to 10);
run;
proc means data=predzip mean;
var p_0;
run;
The parameters of the ZIP model are displayed in Output 11.2.4. The first set of parameters gives the estimates of ![]() in the model for the Poisson process mean. Parameters with the prefix “Inf_” are the estimates of
in the model for the Poisson process mean. Parameters with the prefix “Inf_” are the estimates of ![]() in the logistic model for
in the logistic model for ![]() .
.
Output 11.2.4: ZIP Model Estimation
| Model Fit Summary | |
|---|---|
| Dependent Variable | art |
| Number of Observations | 915 |
| Data Set | WORK.LONG97DATA |
| Model | ZIP |
| ZI Link Function | Logistic |
| Log Likelihood | -1605 |
| Maximum Absolute Gradient | 2.08803E-7 |
| Number of Iterations | 16 |
| Optimization Method | Newton-Raphson |
| AIC | 3234 |
| SBC | 3291 |
| Algorithm converged. |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | t Value | Approx Pr > |t| |
| Intercept | 1 | 0.640838 | 0.121306 | 5.28 | <.0001 |
| fem | 1 | -0.209145 | 0.063405 | -3.30 | 0.0010 |
| mar | 1 | 0.103751 | 0.071111 | 1.46 | 0.1446 |
| kid5 | 1 | -0.143320 | 0.047429 | -3.02 | 0.0025 |
| phd | 1 | -0.006166 | 0.031008 | -0.20 | 0.8424 |
| ment | 1 | 0.018098 | 0.002295 | 7.89 | <.0001 |
| Inf_Intercept | 1 | -0.577060 | 0.509383 | -1.13 | 0.2573 |
| Inf_fem | 1 | 0.109747 | 0.280082 | 0.39 | 0.6952 |
| Inf_mar | 1 | -0.354013 | 0.317611 | -1.11 | 0.2650 |
| Inf_kid5 | 1 | 0.217101 | 0.196481 | 1.10 | 0.2692 |
| Inf_phd | 1 | 0.001272 | 0.145262 | 0.01 | 0.9930 |
| Inf_ment | 1 | -0.134114 | 0.045244 | -2.96 | 0.0030 |
| Analysis Variable : P_0 Probability of art taking level=0 |
|---|
| Mean |
| 0.2985679 |
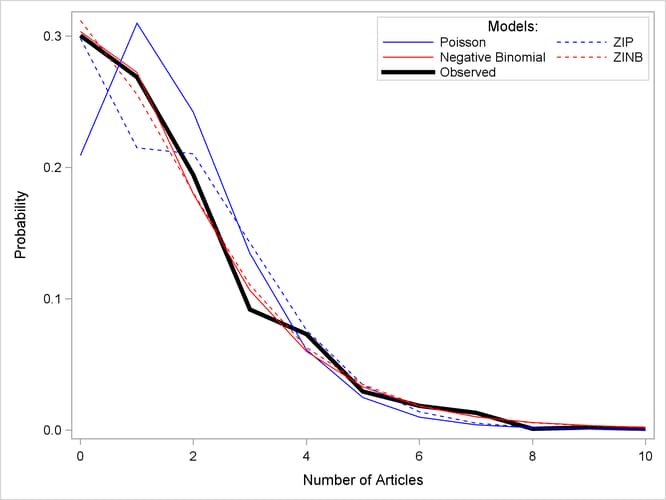
The proportion of zeros predicted by the ZIP model is 0.2986, which is much closer to the observed proportion than the Poisson model. But Output 11.2.6 shows that both models deviate from the observed proportions at one, two, and three articles.
The ZINB model is specified by the DIST=ZINB option. All variables are again used to model both the number of articles and
![]() . The METHOD=QN option specifies that the quasi-Newton method be used to fit the model rather than the default Newton-Raphson
method. These options are implemented in the following statements:
. The METHOD=QN option specifies that the quasi-Newton method be used to fit the model rather than the default Newton-Raphson
method. These options are implemented in the following statements:
proc countreg data=long97data;
model art=fem mar kid5 phd ment / dist=zinb method=qn;
zeromodel art ~ fem mar kid5 phd ment;
output out=predzinb probcount(0 to 10);
run;
proc means data=predzinb mean;
var p_0;
run;
The estimated parameters of the ZINB model are shown in Output 11.2.5. The test for overdispersion again indicates a preference for the negative binomial version of the zero-inflated model (![]() ). The ZINB model also does a good job of estimating the proportion of zeros (0.3119), and it follows the observed proportions
well, though possibly not as well as the negative binomial model.
). The ZINB model also does a good job of estimating the proportion of zeros (0.3119), and it follows the observed proportions
well, though possibly not as well as the negative binomial model.
Output 11.2.5: ZINB Model Estimation
| Model Fit Summary | |
|---|---|
| Dependent Variable | art |
| Number of Observations | 915 |
| Data Set | WORK.LONG97DATA |
| Model | ZINB |
| ZI Link Function | Logistic |
| Log Likelihood | -1550 |
| Maximum Absolute Gradient | 0.00591 |
| Number of Iterations | 81 |
| Optimization Method | Quasi-Newton |
| AIC | 3126 |
| SBC | 3189 |
| Algorithm converged. |
| Parameter Estimates | |||||
|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | t Value | Approx Pr > |t| |
| Intercept | 1 | 0.416747 | 0.143596 | 2.90 | 0.0037 |
| fem | 1 | -0.195507 | 0.075592 | -2.59 | 0.0097 |
| mar | 1 | 0.097583 | 0.084452 | 1.16 | 0.2479 |
| kid5 | 1 | -0.151733 | 0.054206 | -2.80 | 0.0051 |
| phd | 1 | -0.000700 | 0.036270 | -0.02 | 0.9846 |
| ment | 1 | 0.024786 | 0.003493 | 7.10 | <.0001 |
| Inf_Intercept | 1 | -0.191679 | 1.322795 | -0.14 | 0.8848 |
| Inf_fem | 1 | 0.635924 | 0.848902 | 0.75 | 0.4538 |
| Inf_mar | 1 | -1.499439 | 0.938648 | -1.60 | 0.1102 |
| Inf_kid5 | 1 | 0.628412 | 0.442777 | 1.42 | 0.1558 |
| Inf_phd | 1 | -0.037719 | 0.308003 | -0.12 | 0.9025 |
| Inf_ment | 1 | -0.882281 | 0.316219 | -2.79 | 0.0053 |
| _Alpha | 1 | 0.376680 | 0.051029 | 7.38 | <.0001 |
| Analysis Variable : P_0 Probability of art taking level=0 |
|---|
| Mean |
| 0.3119486 |
The following statements compute the average predicted count probability across all scientists for each count 0, 1, ![]() , 10. The averages for each model, along with the observed proportions, are then arranged for plotting by PROC SGPLOT.
, 10. The averages for each model, along with the observed proportions, are then arranged for plotting by PROC SGPLOT.
proc summary data=predpoi;
var p_0-p_10;
output out=mnpoi mean(p_0-p_10)=mn0-mn10;
run;
proc summary data=prednb;
var p_0-p_10;
output out=mnnb mean(p_0-p_10)=mn0-mn10;
run;
proc summary data=predzip;
var p_0-p_10;
output out=mnzip mean(p_0-p_10)=mn0-mn10;
run;
proc summary data=predzinb;
var p_0-p_10;
output out=mnzinb mean(p_0-p_10)=mn0-mn10;
run;
data means;
set mnpoi mnnb mnzip mnzinb;
drop _type_ _freq_;
run;
proc transpose data=means out=tmeans;
run;
data allpred;
merge obs(where=(art<=10)) tmeans;
obs=percent/100;
run;
proc sgplot;
yaxis label='Probability';
xaxis label='Number of Articles';
series y=obs x=art / name='obs' legendlabel='Observed'
lineattrs=(color=black thickness=4px);
series y=col1 x=art / name='poi' legendlabel='Poisson'
lineattrs=(color=blue);
series y=col2 x=art/ name='nb' legendlabel='Negative Binomial'
lineattrs=(color=red);
series y=col3 x=art/ name='zip' legendlabel='ZIP'
lineattrs=(color=blue pattern=2);
series y=col4 x=art/ name='zinb' legendlabel='ZINB'
lineattrs=(color=red pattern=2);
discretelegend 'poi' 'zip' 'nb' 'zinb' 'obs' / title='Models:'
location=inside position=ne across=2 down=3;
run;
For each of the four fitted models, Output 11.2.6 shows the average predicted count probability for each article count across all scientists. The Poisson model clearly underestimates the proportion of zero articles published, while the other three models are quite accurate at zero. All of the models do well at the larger numbers of articles.
Output 11.2.6: Average Predicted Count Probability