The FORECAST Procedure

Ahlburg, D. A. (1984). “Forecast Evaluation and Improvement Using Theil’s Decomposition,” Journal of Forecasting, 3, 345–351.

Aldrin, M. and Damsleth, E. (1989). “Forecasting Non-Seasonal Time Series with Missing Observations,” Journal of Forecasting, 8, 97–116.

Archibald, B.C. (1990), “Parameter Space of the Holt-Winters’ Model,” International Journal of Forecasting, 6, 199–209.

Bails, D.G. and Peppers, L.C. (1982), Business Fluctuations: Forecasting Techniques and Applications, New Jersey: Prentice-Hall.

Bartolomei, S.M. and Sweet, A.L. (1989). “A Note on the Comparison of Exponential Smoothing Methods for Forecasting Seasonal Series,” International Journal of Forecasting, 5, 111–116.

Bureau of Economic Analysis, U.S. Department of Commerce (1992 and earlier editions), Business Statistics, 27th and earlier editions, Washington: U.S. Government Printing Office.

Bliemel, F. (1973). “Theil’s Forecast Accuracy Coefficient: A Clarification,” Journal of Marketing Research, 10, 444–446.

Bowerman, B.L. and O’Connell, R.T. (1979), Time Series and Forecasting: An Applied Approach, North Scituate, Massachusetts: Duxbury Press.

Box, G.E.P. and Jenkins, G.M. (1976), Time Series Analysis: Forecasting and Control, Revised Edition, San Francisco: Holden-Day.

Bretschneider, S.I., Carbone, R., and Longini, R.L. (1979). “An Adaptive Approach to Time Series Forecasting,” Decision Sciences, 10, 232–244.

Brown, R.G. (1962), Smoothing, Forecasting and Prediction of Discrete Time Series, New York: Prentice-Hall.

Brown, R.G. and Meyer, R.F. (1961). “The Fundamental Theorem of Exponential Smoothing,” Operations Research, 9, 673–685.

Chatfield, C. (1978). “The Holt-Winters Forecasting Procedure,” Applied Statistics, 27, 264–279.

Chatfield, C., and Prothero, D.L. (1973). “Box-Jenkins Seasonal Forecasting: Problems in a Case Study,” Journal of the Royal Statistical Society, Series A, 136, 295–315.

Chow, W.M. (1965). “Adaptive Control of the Exponential Smoothing Constant,” Journal of Industrial Engineering, September–October 1965.

Cogger, K.O. (1974). “The Optimality of General-Order Exponential Smoothing,” Operations Research, 22, 858–.

Cox, D. R. (1961). “Prediction by Exponentially Weighted Moving Averages and Related Methods,” Journal of the Royal Statistical Society, Series B, 23, 414–422.

Fair, R.C. (1986). “Evaluating the Predictive Accuracy of Models,” In Handbook of Econometrics, Vol. 3., Griliches, Z. and Intriligator, M.D., eds. New York: North Holland.

Fildes, R. (1979). “Quantitative Forecasting—The State of the Art: Extrapolative Models,” Journal of Operational Research Society, 30, 691–710.

Gardner, E.S. (1984). “The Strange Case of the Lagging Forecasts,” Interfaces, 14, 47–50.

Gardner, E.S., Jr. (1985). “Exponential Smoothing: The State of the Art,” Journal of Forecasting, 4, 1–38.

Granger, C.W.J. and Newbold, P. (1977), Forecasting Economic Time Series, New York: Academic Press, Inc.

Harvey, A.C. (1984). “A Unified View of Statistical Forecasting Procedures,” Journal of Forecasting, 3, 245–275.

Ledolter, J. and Abraham, B. (1984). “Some Comments on the Initialization of Exponential Smoothing,” Journal of Forecasting, 3, 79–84.

Maddala, G.S. (1977), Econometrics, New York: McGraw-Hill.

Makridakis, S., Wheelwright, S.C., and McGee, V.E. (1983). Forecasting: Methods and Applications, 2nd Ed. New York: John Wiley and Sons.

McKenzie, Ed (1984). “General Exponential Smoothing and the Equivalent ARMA Process,” Journal of Forecasting, 3, 333–344.

Montgomery, D.C. and Johnson, L.A. (1976), Forecasting and Time Series Analysis, New York: McGraw-Hill.

Muth, J.F. (1960). “Optimal Properties of Exponentially Weighted Forecasts,” Journal of the American Statistical Association, 55, 299–306.

Pierce, D.A. (1979). “ 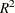Measures for Time Series,” Journal of the American Statistical Association, 74, 901–910.

Pindyck, R.S. and Rubinfeld, D.L. (1981), Econometric Models and Economic Forecasts, Second Edition, New York: McGraw-Hill.

Raine, J.E. (1971). “Self-Adaptive Forecasting Reconsidered,” Decision Sciences, 2, 181–191.

Roberts, S.A. (1982). “A General Class of Holt-Winters Type Forecasting Models,” Management Science, 28, 808–820.

Theil, H. (1966). Applied Economic Forecasting. Amsterdam: North Holland.

Trigg, D.W., and Leach, A.G. (1967). “Exponential Smoothing with an Adaptive Response Rate,” Operational Research Quarterly, 18, 53–59.

Winters, P.R. (1960). “Forecasting Sales by Exponentially Weighted Moving Averages,” Management Science, 6, 324–342.